Правила композиции в фотографии. Золотое сечение
О композиции, Золотом Сечении и числах Фибоначчи
Золотое сечение - деление непрерывной величины на две неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей. Или меньший отрезок так относится к большему, как больший ко всему.
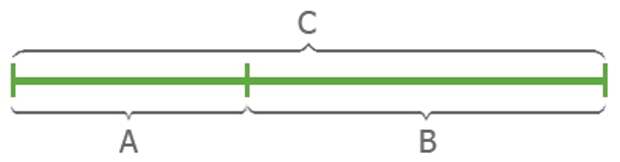
Термин золотое сечение был введен Леонардо да Винчи, который использовал его, как пропорции «идеального человеческого тела».
Например, пропорции мужского тела колеблются в пределах отношения 13 : 8 = 1,625 и немного ближе подходят к золотому сечению, чем пропорции женского тела, выражающиеся в соотношении 8 : 5 = 1,6. Итак, самым гармоничным соотношением является значение 1.618
Золотое сечение можно найти практически везде в живой природе.
Можно увидеть его и в самых удачных творениях человеческих рук - принципы золотого сечения легли в основу композиционного построения многих произведений мирового искусства.
Например, в рельефе из храма фараона Сети в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции и т. д..
Под «правилом золотого сечения» в архитектуре и искусстве обычно понимаются асимметричные композиции, не обязательно содержащие золотое сечение математически.
«Есть вещи, которые нельзя объяснить. Вот Вы подходите к пустой скамейке и садитесь на нее. Где Вы сядете – посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно Вашего тела, будет равно 1,62. Простая вещь, абсолютно инстинктивная… Садясь на скамейку, Вы произвели «золотое сечение». Анхель де Куатье
Давайте проведем эксперимент: какой прямоугольник из ниже расположенных, с вашей точки зрения, имеет идеальные пропорции?
По результатам опросов, большинство людей признает самым гармоничным прямоугольник под номером 2. Именно он построен в соответствии с правилом «золотого сечения».
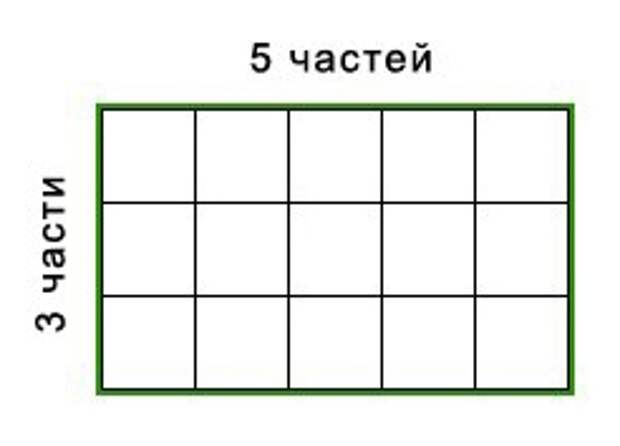
Золотое сечение можно вычислить очень просто, без геометрии и алгебры, — для этого используют приближенные значения 0,62 и 0,38. Если целый отрезок принять за 100 частей, то большая часть отрезка равна 62, а меньшая — 38 частям.
Или вспомнив ряд Фибоначчи - ряд чисел, в котором каждое последующее число равно сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 1З, 21 и т. д.
Этот ряд был открыт итальянским математиком Фибоначчи и назван его именем. Он обладает тем свойством, что отношения между соседними числами по мере возрастания чисел ряда, все более приближаются к 1,618, то есть к отношению золотого сечения.
Числа ряда Фибоначчи часто используются в дизайне для вычисления пропорций, т.к. работать с ними легче, чем с числом 1,618.
Вот еще пара удобных приложений, которые помогут вычислить Золотое сечение.
Phiculator - http://www.thismanslife.co.uk/main.asp?contentid=phiculator – маленькая и удобная программка, которая из любого введенного числа, автоматически вычислит, соответствующее Золотому сечению, значение.
Golden Section Ratio Design Tool - http://www.atrise.com/golden-section – а это уже солидный инструмент, который поможет избежать рутинных операций при работе с компоновкой объектов и форм. Результат можно увидеть на лету.
Вы можете спросить, зачем дизайнеру эта математика и какой в ней практический смысл? А смысл есть. Например, отношение сторон у iPod Shuffle 1.59, iPod Classic 1.67, а у iPhone4 1.7 – объем продаж за первые 4 дня торговли превысил 1 миллион 700 тысяч штук.
Понятно, что поклонники iPod оценивают его по другим характеристикам.
Но, может быть не случайно дизайнеры Apple выбрали для своего детища именно такие пропорции?
Золотое сечение встречается в предметном мире в качестве базового конструктивного принципа, а знание и применение Золотого Сечения поможет Вам в любой сфере, чем бы Вы не занимались.
Но, вернемся к дизайну…
Итак, принцип золотого сечения на практике в Web поможет нам определить, какого размера должны быть элементы на странице, в каком месте и на каком расстоянии они должны располагаться друг от друга, чтобы не нарушать баланс, чтобы наш сайт выглядел гармоничным.
Воспользуемся правилом третей, основанном на применении золотого сечения или цифр ряда Фибоначчи. Это правило позволит нам вычислить центры внимания на странице.
Для этого поделим страницу на три части по горизонтали и вертикали.
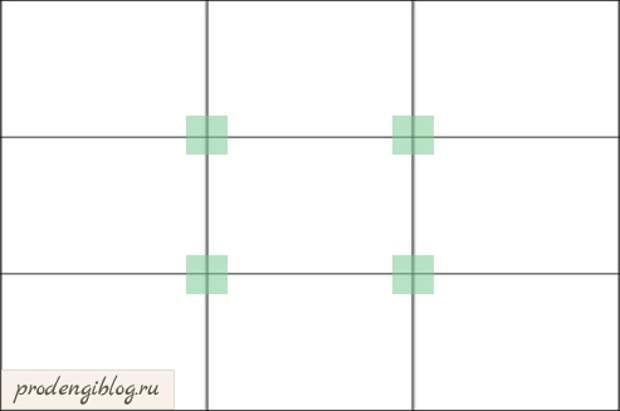
На пересечении линий находятся 4 важные точки, которые можно использовать для выделения основных деталей макета сайта.
Как правило, не стоит использовать сразу все четыре точки, но, одну или две – обязательно.
Какую то важную деталь лучше поместить в левый верхний угол, т. к. пользователи начинают просматривать сайт именно оттуда – логотип, если у нас имиджевый сайт или телефоны и др. контактную информацию, если сайт продающий.
Навигационное меню можем расположить на первой горизонтальной линии.
Еще один-два важных элемента располагаем на точках пересечения горизонтальных и вертикальных линий.
Что нам дало такое расположение блоков?
Мы поместили наиболее важные вещи в местах наибольшего внимания пользователя. При таком расположение элементов, наш сайт становится более удобным и более структурированным для просмотра.
Что это дает нам, как владельцам сайта?
Например, дополнительный доход - если мы разместим рекламные блоки в тех местах, где их с большей вероятностью увидят посетители сайта.
Или больше отзывов на посты, если в нужном месте указать какой нибудь стимул для комментирования, вроде блока "Топ комментаторов".
2/3 страницы займет центральная колонка и 1/3 отведем под сайдбар.
Еще один пример – создадим 3х колоночный шаблон.
Разделим по предыдущему принципу страницу на 2 колонки.
А дальше центральную колонку опять поделим вертикальными линиями на 3 равные части, первая из которых будет сайдбаром, а 2 остальные центральной частью.
В первом сайдбаре можно расположить основное меню сайта, содержащее самые важные ссылки. Их посетитель сайта увидит в первую очередь, (поскольку он привык читать текст слева направо), а всякую дополнительную информацию поместить во второй сайдбар.
К сожалению, чтобы сделать красивый шаблон описанного выше правила недостаточно - нужно еще выбрать подходящие цвета.
О подборе цвета для сайта читайте дальше - Как подобрать цвет для сайта: немного о теории цвета.
А еще, чтобы ваш сайт отличался от сотен тысяч других сайтов, в нем должна быть своя изюминка, так что в любом случае соль и сахар по вкусу 
В статье использованы материалы сайтов: http://www.smashingmagazine.com, http://seleckis.lv/journal, http://designinfoline.ru
Известно, что по-настоящему наш взгляд радуют изображения, в основу геометрии которых положено золотое сечение. Значит, Вам нужно, как минимум, подобрать размеры сайта, который находятся в отношении "божественной пропорции". Для этого у Вас есть две возможности. Первая - возьмите калькулятор, с помощью которого сможете легко умножить или разделить данный размер на 1,618. Вторая - Вы можете воспользоваться бесплатными или платными (есть и такие!) инструментами, которые позволяют быстро вычислить "золотое сечение". Главное преимущество таких средств - наглядность результата.
Правило Оккама "не умножай сущностей сверх необходимого" в нашем случае означает, что чаще всего простые инструменты оказываются самыми востребованными.
Поэтому с самого начала хочу обратить ваше внимание на PhiCulator - бесплатный калькулятор золотого сечения. Возможно, Вам сейчас стало интересно "Почему этот калькулятор так странно называется?" Ничего странного нет. Наоборот, все просто: в математике золотое сечение принято обозначать греческой буквой "фи". Отсюда и название.
Использовать Фикулятор тоже просто: вводите исходное число в нижний квадрат (там, где на картинке стоит единица) и в верхнем (большем) квадрате сразу получаете второе число, равное данному числу, умноженному на 1.618033988749. Если же ввести данное число в верхний квадрат (туда, где на картинке 1.618033988749), то в нижнем квадрате получите результат, деленный на 1.618033988749.
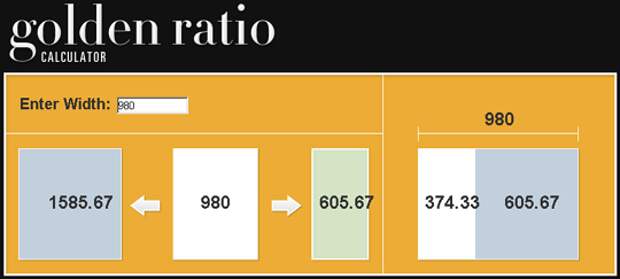
На втором месте (у меня - на первом) - Golden Ratio Calculator - бесплатный онлайн инструмент, сделанный специально для веб-дизайнеров. Как им пользоваться, уверен, разберетесь сами:
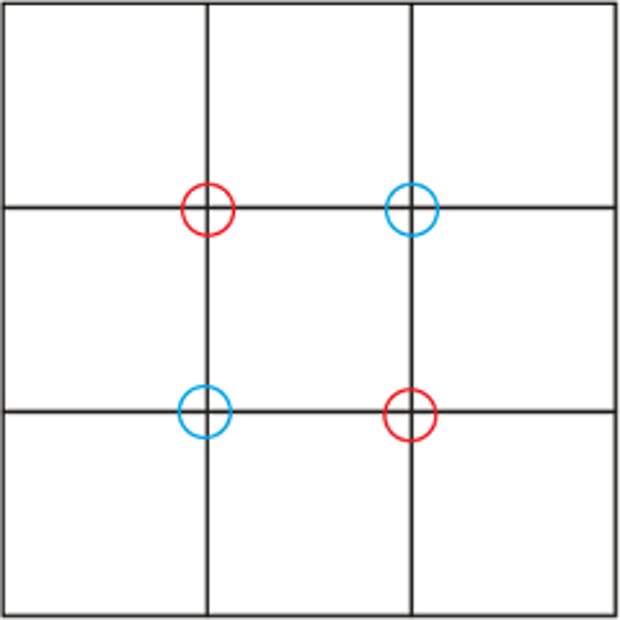
Вместо золотого сечения "ленивые" веб-дизайнеры часто используют упрощенный вариант "божественной пропорции", так называемое "правило третей". Этим правилом пользуются также фотохудожники. Правило третей состоит в том, что вся композиция делится на девять равных частей. Для этого нанесите на рисунок четыре прямых линии, две горизонтальных и две вертикальных, так, что получится сетка из девяти равных прямоугольников. Четыре точки, в которых пересекаются эти линии - это точки, которые притягивают взгляд, именно в них должны размещаться наиболее значимые элементы изображения. Верхняя левая точка считается наиболее важной. Правая нижняя - на втором месте. Три вертикальных столбца равной ширины задают приятное глазу вертикальное деление веб-страницы на колонки. По-возможности, этот же принцип нужно использовать и для горизонтального деления веб-страницы. К каждому элементу полученной исходной сетки в свою очередь можно применить "правило третей", наложив на него сетку 3х3 соответствующего размера. Получится более сложная, так называемая модульная сетка.
Если Вы не хотите всей этой мороки, то можете просто скачать скрипт, который автоматически генерирует шаблоны модульной сетки с сайта 960 Grid System. Вот пример сетки, которую генерирует этот скрипт.
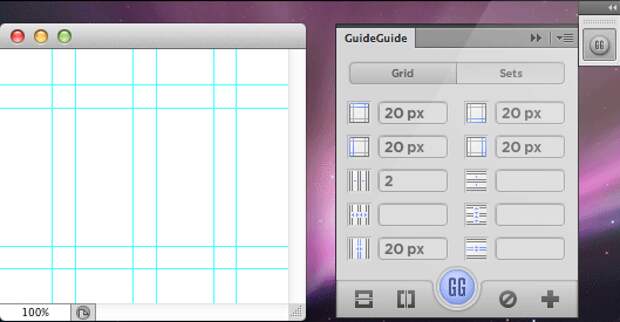
Если же этот вариант Вас не устраивает, а с Фотошопом Вы на ты, то в качестве альтернативы могу посоветовать еще одно - установите GuideGuide - бесплатный плагин для автоматического создания модульных сеток в Adobe Photoshop:
Как использовать плагин GuideGuide? Небольшой мануал по-русски нашелся здесь.
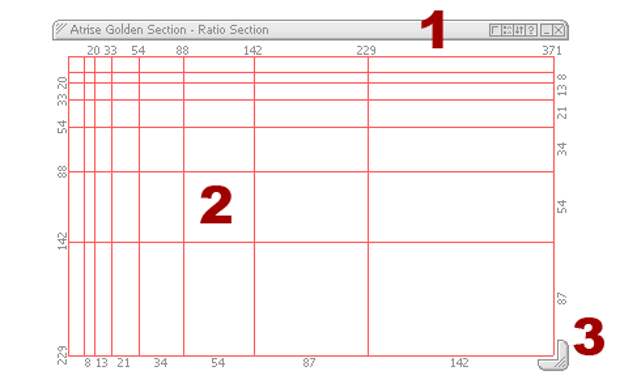
Если же обычные бесплатные средства создания модульных сеток Вас по каким-либо причинам не устраивают, и Вы обязательно хотите чего-нибудь на эту же тему, но покруче, тогда попробуйте Atrise Golden Section. Это замечательная программа в своем роде. Ее возможности по построению модульных сеток и не только простираются далеко за пределы тривиального веб-дизайна. Atrise Golden Section по заслугам оценят и художники, фотографы, и программисты, и даже брокеры. Хотя программа Atrise Golden Section платная, но на сайте имеется ее 30-дневная триал-версия. Этого вполне хватит, чтобы сверстать дизайн Вашего сайта.
Вот один из скринов Atrise Golden Section, который иллюстрирует возможности программы:
Золотое сечение в живописи
Исследуя композиционную структуру картин - шедевров мирового изобразительного искусства, искусствоведы обратили внимание на тот факт, что в пейзажных картинах широко используется закон золотого сечения. Примером такой картины является картина И.И. Шишкина "Корабельная роща".
На этой знаменитой картине с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит картину золотым сечением по горизонтали. Справа от сосны - освещенный солнцем пригорок. Он делит картину золотым сечением по вертикали. Слева от главной сосны находится много сосен - при желании можно с успехом продолжить деление золотым сечением по горизонтали левой части картины. Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия в соответствии с замыслом художника.
Тот же принцип мы видим в картине И.Е. Репина "А.С. Пушкин на акте в Лицее 8 января 1815 года".
Фигура Пушкина помещена художником в правой части картины по линии золотого сечения. Левая часть картины, в свою очередь, тоже разделена в пропорции золотого сечения: от головы Пушкина до головы Державина и от нее до левого края картины. Расстояние от головы Державина до правого края картины разделено на две равные части линией золотого сечения, проходящей вдоль фигуры Пушкина.
Еще один пример - картина Н.Н. Ге "Александр Сергеевич Пушкин в селе Михайловском".
В этой картине фигура Пушкина также поставлена художником слева на линии золотого сечения. Композиционное построение картины подобно картине Репина. Голова военного, с восторгом слушающего чтение поэта, находится на другой вертикальной линии золотого сечения.
Широко использовал золотое сечение в своем творчестве талантливый русский художник Константин Васильев, рано ушедший из жизни. Еще будучи студентом Казанского художественного училища, он впервые услышал о "золотом сечении". И с тех пор, приступая к каждой своей работе, он всегда начинал с того, что мысленно пытался определить на холсте ту основную точку, куда должны были стягиваться, как к невидимому магниту, все сюжетные линии картины. Ярким примером картины, построенной "по золотому сечению", является картина "У окна".
О чем хотел поведать нам художник в этой картине? Об этом можно лишь догадываться. Одно бесспорно - перед нами жизнь как она есть. То, что двое этих молодых людей бесконечно любят друг друга, мы понимаем при первом взгляде на картину. Но если он весь во власти своего неудержимого порыва, готов отстаивать свою любовь перед кем угодно, то ее чувства что-то сдерживает. Что именно - страх, гордыня, верность родовым традициям: А может быть, наитие, природное чутье, более свойственное женскому сердцу, подсказывает ей, что не время им сейчас думать о любви?
Как бы там ни было, главная мысль этой картины, вся кульминация ее заложена именно в образе девушки, чье лицо озарено удивительной чистотой, достоинством и еще спокойной мудростью. И лицо девушки художник разместил в "золотой" точке картины, которая находится на пересечении двух "золотых" линий - горизонтальной и вертикальной, которые в точности проходят через глаз девушки. И это композиционное решение является одной из причин ощущения удивительной гармонии, которой наполнена картина, олицетворяющая все те исконные начала, которые всегда делали русскую женщину прекрасной.
И еще об одном композиционном приеме, которым широко пользовались художники эпохи Возрождения. Речь идет об использовании художниками "филлотаксисных" растровых решеток. Мы уже рассказывали об удивительном ботаническом явлении - филлотаксисе, в соответствии с которым природа конструирует сосновые шишки, ананасы, головки подсолнечника, кактусы и многие другие ботанические структуры.
В соответствии с законами филлотаксиса ареолы (скопления колючек) кактуса располагаются по спиралям, причем число левых и правых спиралей для кактуса являются соседними числами Фибоначчи 21 и 34. Если теперь посмотреть на тот же кактус со стороны, то обнаруживается, что спирали на сравнительно небольшом участке поверхности выглядят как прямые линии, идущие по диагонали сверху вниз и слева направо или снизу вверх и справа налево. На фотографии хорошо видно, что прямые, идущие в правом направлении, имеют меньший наклон, чем прямые, идущие в левом направлении. При этом число правых и левых диагоналей связаны фибоначчиевой зависимостью. Действительно на фотографии отчетливо видно, что вначале примерно на 2 диагонали с правым наклоном приходится 3 диагонали с левым наклоном (2:3), затем на 3 правых диагонали 5 левых (3:5) и т.д.
Геометрическая модель рассмотренного на фотографии участка кактуса представлена ниже в виде растровой сетки, в которой наклонные линии (с правым и левым наклоном) моделируют принцип расположения ареолов на поверхности кактуса.
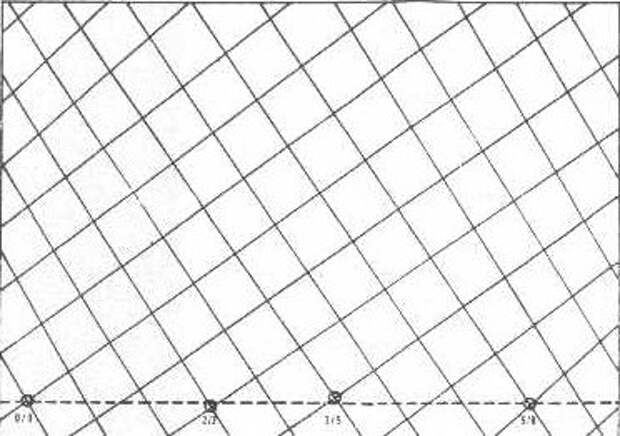
Если теперь представить развертку поверхности всего кактуса на плоскости, то мы получим подобную растровую сетку, в которой имеется 21 диагоналей с правым наклоном и 34 диагоналей с левым наклоном. Созданная таким образом сеть линий ("филлотаксисная растровая сетка") оказывается в эстетическом отношении столь же оптимальной, как и прямоугольник, построенный по принципу золотого сечения. Комплекс линий, имеющих вполне определенный и в то же время различный наклон, придает полю изображения эмоциональное внутреннее напряжение и одновременно строгую уравновешенность. Эти принципы композиционного построения художественного произведения присущи многим полотнам старых мастеров живописи.
Австрийский ученый Ф. Патури, автор замечательной книги "Растения - гениальные инженеры природы", провел анализ использования растровых сеток в произведениях великих художников. Для этого он наложил растровую сетку на репродукцию картины Тициана "Вакх и Ариадна".
Анализ картины с учетом "филлотаксистной" растровой сетки привел Патури к следующему заключению:
"Все основные линии перспективы совпадают с растром. Даже множество второстепенных для сюжета деталей и форм художник поместил в то поле внутреннего напряжения, на котором и построена картина. Обратите внимание на виднеющийся на горизонте небольшой холм в правой стороне полотна рядом с церковной колокольней, на ветви большого дерева, на очертание кучевого облака, лежащего под созвездием, на задние лапы и линию живота крупной дикой кошки, на направление оси перекинутой вазы, на воздетую правую руку сатира в венке из виноградных лоз в правом углу холста и, наконец, на поднятую ногу лошади".
Тому, кто посчитает это делом случая или полагает, что картина Тициана является исключением, мы рекомендуем перенести растровую сетку на прозрачную бумагу и затем наложить ее на репродукции некоторых художественных полотен. Он будет изумлен тем, насколько часто композиции картин станут повторять динамику золотого сечения вплоть до ее зеркального отражения". Такие произведения, как "Ливийская сивилла" Микеланджело, "Поклонение пастухов" Тинторетто, "Мадонна с длинной шеей" Пармиджанино, "Азия" Тьеполо (зеркальное отражение!), "Вакханалия" Пуссена, "Драка крестьян при игре в карты" Брауэра или "Праздник любви" Ватто (зеркальное отражение!), - это немногие примеры, которые лишь подтверждают общую закономерность.
И далее Патури делает следующее важное заключение:
"Во все времна художники, осознанно или неосознанно, учились постигать законы эстетического восприятия, наблюдая природу. Живописцев всегда пленяла простая и одновременно рациональная геометрия форм биологического роста".
http://www.goldenmuseum.com/0805Painting_rus.html
Золотое сечение
Урок ведет математик Лазарь Людмила Павловна.
Цель: сегодня мы раскроем тайны “золотого сечения”. Узнаем, что существует такая золотая точка на любом отрезке, которая обеспечивает, присутствие красоты, соразмерности всех частей, рассмотрим примеры где встречается “золотое сечение” в живой и не живой природе. Проведем практическую работу на нахождения “золотого сечения”.
“Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении … Первое можно сравнить с мерой золота ; второе же больше напоминает драгоценный камень.”
Иоганн Кеплер
Теорему Пифагора знает каждый, а вот что такое “золотое сечение” – далеко не все. Расскажем вам об этом “драгоценном камне”.
Итак – “золотое сечение” – это такое деление целого на две неравные части, при котором
целое так относится к большей части, как большая к меньшей.
Рассмотрим деление отрезка на части в отношении равном “золотому сечению”.
Пусть точка М делит отрезок АВ в золотом отношении.
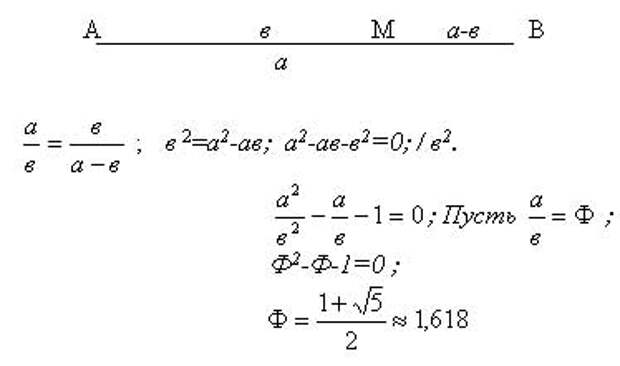
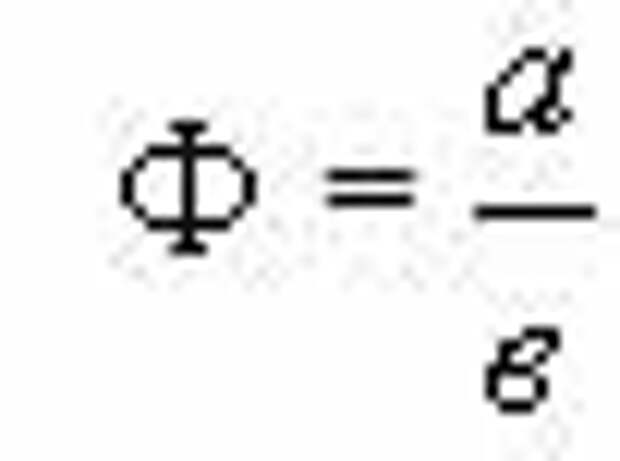. Такое обозначение принято в честь древнегреческого скульптора Фидия, жившего в V веке до н.э.
Итак “золотое сечение” – это иррациональное число, оно приблизительно равно 1,618.
Задача 1. Возьмите отрезок длиной 10 см и разделите его приблизительно в золотом отношении.
(6,2 см и 3,8 см) одна часть отрезка больше другой в 1,6 раза.
Части “золотого сечения” составляют приблизительно 62% и 38% всего отрезка.
В эпоху Возрождения “золотое сечение2 было очень популярным среди художников, скульпторов , архитекторов. Так, выбирая размеры картины, художники старались, чтобы отношение ее сторон равнялось Ф. Такой прямоугольник стали называть “золотым”.
Задача 2. Построим золотой прямоугольник.
- Начертим квадрат и разделим его на два равных прямоугольника.
- В одном из прямоугольников проведем диагональ АВ.
- Циркулем проведем окружность радиуса АВ с центром в точке А.
- Продолжим основание квадрата до пересечения с дугой в точке Р и проведем под прямым углом вторую сторону искомого прямоугольника.
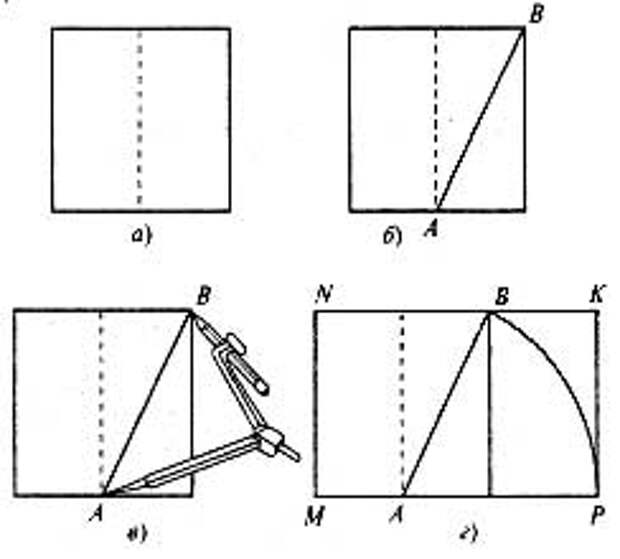
Измерьте линейкой длины сторон построенного прямоугольника MNKP и вычислите отношения большей стороны к меньшей. (Отношение сторон должно быть примерно равно 1,6).
Но как же разделить отрезок в золотом отношении?
С помощью непосредственных измерений сделать это не возможно, поскольку число Ф–иррациональное. Древние мастера использовали циркуль и линейку, причем были найдены различные способы построения. Рассмотрим один из них, самый простой.
Пусть дан отрезок АВ , и надо осуществить его “золотое сечение”. Проведем перпендикуляр к отрезку АВ (будем считать, что АВ=1) и отложим на нем отрезок ВД = 2АВ. Тогда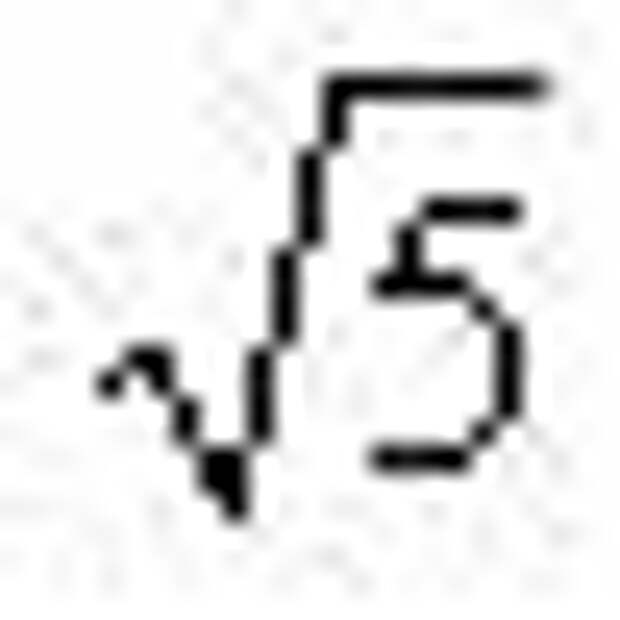 
=АД. Из точки Д проведем окружность радиусом ДК, где ДК=АВ.
Тогда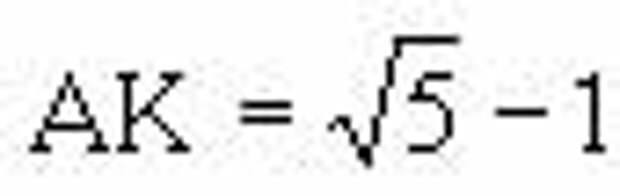 
. Теперь проведем окружность с центром в точке А радиусом 
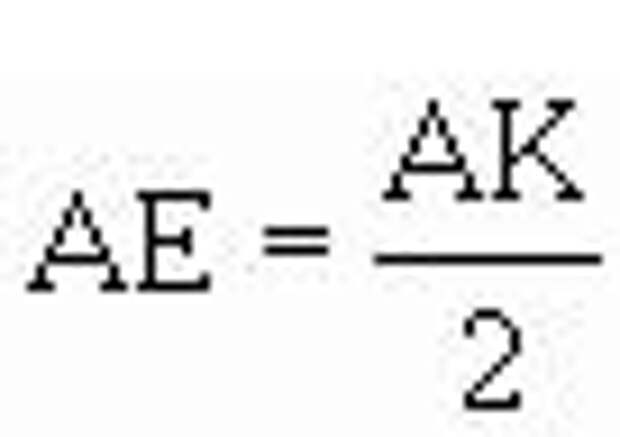Она пересечет отрезок АВ в точке С золотого сечения, поскольку АС= 
.
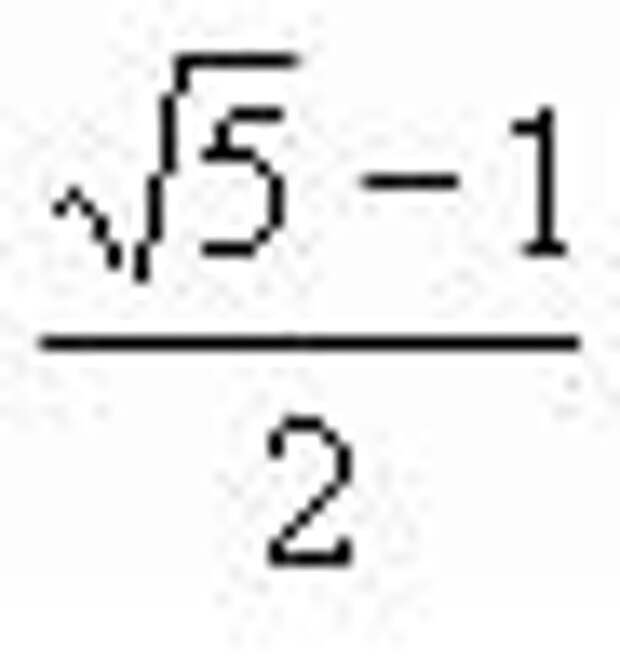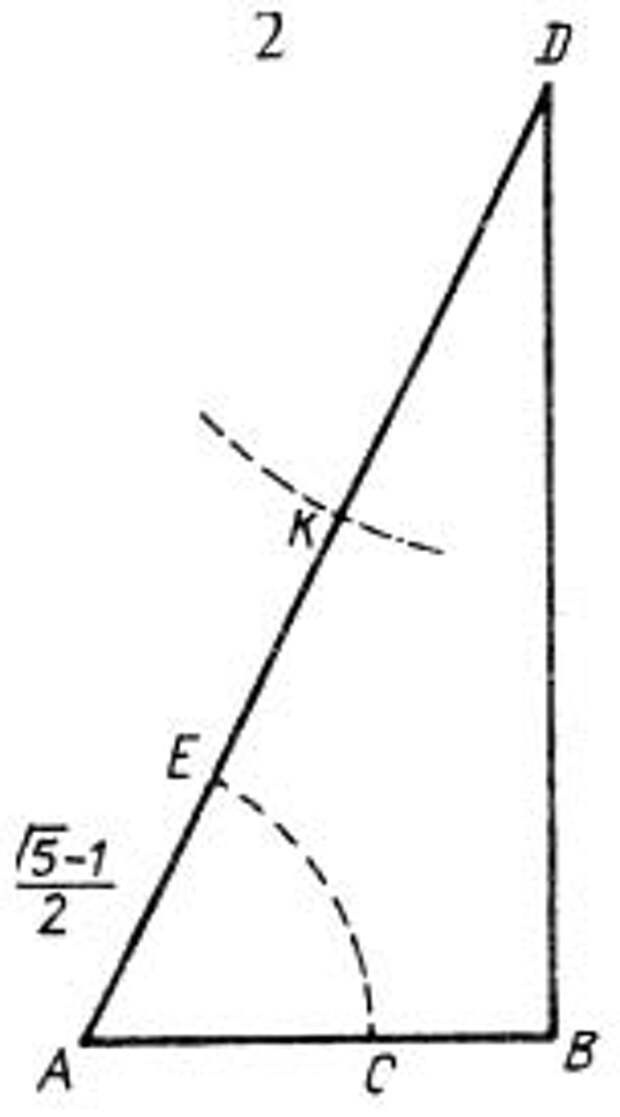
Итак, найдена, казалось бы, совершенно ординарная точка на обычном отрезке. А между тем ею обеспечивается присутствие красоты, соразмерности всех частей.
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V век до н.э.).
Строительством храма Парфенон руководил архитектор Фидий (краткое сообщение о этом произведении).
Парфенон — главный храм в древних Афинах, посвященный покровительнице этого города и всей Аттики, богине Афине-Девственнице (
). Он красовался на самом высоком пункте афинского акрополя, там, где перед тем стоял не вполне достроенный храм той же богини, заложенный еще до нашествия. По окончании персидских войн, в правление Перикла, приступили к сооружению, на месте прежнего святилища, нового, более обширного и роскошного храма, при чем пущено в ход искусство лучших из тогдашних художников и употреблены огромные денежные средства. Строителями П. называют Иктина и Калликрата; первому, по-видимому, принадлежал проект этого здания, а второй заведовал производством строительных работ. Велики скульптор Фидий и сам Перикл наблюдали за постройкой, продолжавшейся около десяти лет, с 448 по 438 г. До Р. Хр. На прямоугольной платформе (в 68,4 м длины и в 30,38 м ширины), сложенной из пирейского камня и на которую можно было со всех сторон подниматься по трем ступеням, высился построенный из пентелийского мрамора величественный периптер дорического стиля с восемью колоннами в каждом коротком фасе и с семнадцатью в каждом длинном. Вышиной эти колонны были в 11 м, диаметр их разреза в нижнем конце равнялся 1,8 м. Окруженный этой колоннадой, стоит и посей день.
Отношение длины здания Парфенона в Афинах к его высоте равно Ф (фи).
КВ: АВ = СВ :АС= АВ:ВС = Ф.
Другим примером из архитектурной древности является Пантеон, храм всех богов в Риме.
Известный русский архитектор Казаков Матвей Федорович в своем творчестве широко использовал “золотое сечение”. Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например золотое сечение можно обнаружить в архитектуре здания сената в Кремле. По проекту Казакова построена в Москве Голицынская больница, которая в настоящее время называется “Первая клиническая” больница имени Пирогова.
Петровский дворец в Москве. Построен по проекту М.Ф. Казакова.
Еще один архитектурный шедевр Москвы – дом Пашкова (1786 г.)– является одним из наиболее совершенным произведением архитектуры Василия Ивановича Баженова.
Прекрасное творение прочно вошло в ансамбль центра современной Москвы. Наружный вид сохранился почти без изменения до наших дней, ныне Российская государственная библиотека.
Многие высказывания зодчего заслуживают внимания и в наши дни. О своем любимом искусстве В. Баженов говорил: “Архитектура – главнейшие имеет три предмета: красоту, спокойность и прочность здания … К достижению сего служит руководством знание пропорции , перспективы , механики или вообще физики ,а всем им общим вождем является рассудок”
Внимание людей издавна привлекала совершенство формы пятиконечная звезда.
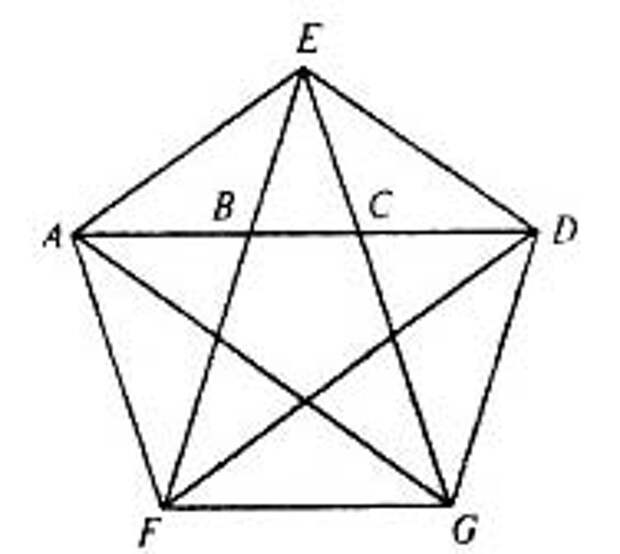
Пятиконечной звезде - около 3000 лет. Ее первые изображения донесли до нас вавилонские глиняные таблички. Из древней Вавилонии в Средиземноморье, как полагают, звездчатый пятиугольник перевез Пифагор и сделал его символом жизни и здоровья, а также тайным опознавательным знаком.
Сегодня пятиконечная звезда реет на флагах едва ли не половины стран мира. Чем же объясняется такая популярность? Тем, что совершенная форма этой фигуры радует глаз. Звездчатый пятиугольник буквально соткан из пропорций, и прежде всего золотой пропорции.
Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей их подвиги и деяния.
Известно, что еще в древности основу скульптуры составляла теория пропорции. Отношение частей человеческого тела связывалось с формулой “золотого сечения”.
Пропорции “золотого сечения” создают впечатления гармонии красоты, поэтому скульпторы использовали их в своих произведениях.
Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения”. Так например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям.
Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих произведениях.
Самая знаменитая из них была статуя Зевса Олимпийского, которая считалась одним из чудес света и статуя Афины Парфенос.
Измерения нескольких тысяч человеческих тел позволило обнаружить, что для взрослых мужчин это отношение равно 13:8=1,625, а взрослых женщин оно составляет 8:5 = 1,6. Так что пропорции мужчин ближе к “золотому сечению”.
“Золотое сечение” в изобразительном искусстве.
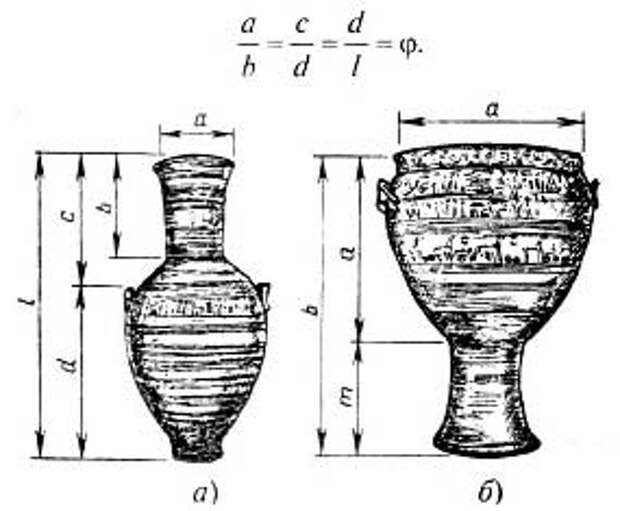
Особый вид изобразительного искусства Древней Греции следует выделить изготовление и роспись всевозможных сосудов. В изящной форме легко угадываются пропорции золотого сечения .
В живописи и скульптуре храмов, на предметах домашнего обихода древние египтяне чаще всего изображали богов и фараонов. Были установлены каноны изображения стоящего человека идущего, сидящего и т.д. Художники обязаны были заучивать отдельные формы и схемы изображения по таблицам и образцам. Художники Древней Греции совершали специальные путешествия в Египет, чтобы поучиться умению пользоваться каноном.
Перед вами канон изображения стоящего человека, все пропорции человека связаны формулой “золотого сечения”.
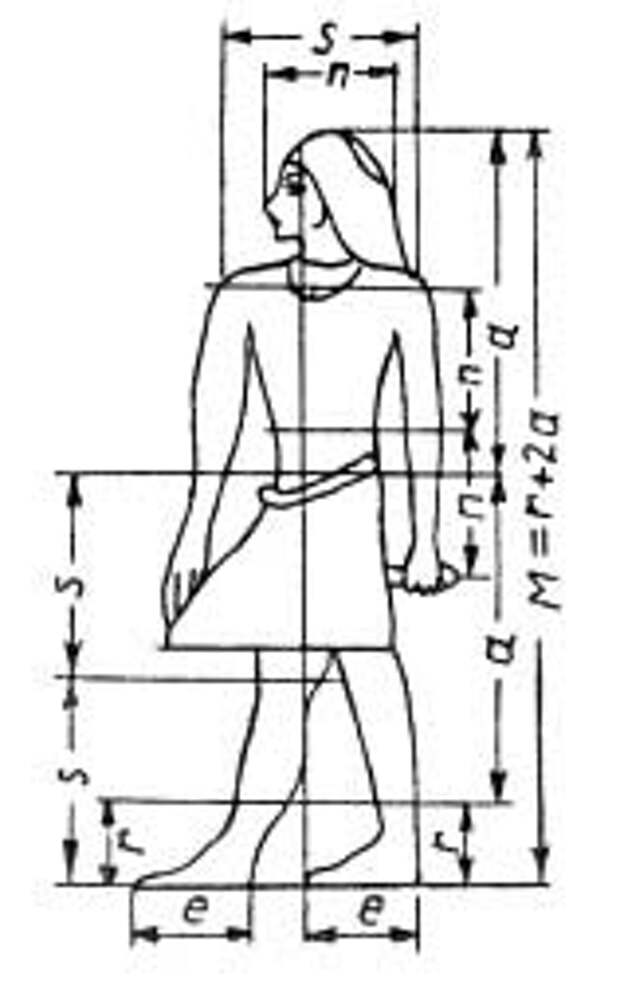
Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.
Леонардо да Винчи
Его личность одна из загадок истории. Сам Леонардо да Винчи говорил : “Пусть никто, не будучи математиком, не дерзнет читать мои труды”. Сам термин “золотое сечение” ввел Леонардо да Винчи. Он говорил о пропорции человеческого тела.
“Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.
В наиболее известной картине Леонардо, портрете Моны Лизы (так называемой “Джоконды”, около 1503, Лувр) образ богатой горожанки предстает таинственным олицетворением природы как таковой, не теряя при этом чисто женского лукавства; внутреннюю значительность композиции придает космически-величавый и в то же время тревожно-отчужденный пейзаж, тающий в холодной дымке. Ее композиция основана на золотых треугольниках, которые являются частями правильного звездчатого пятиугольника.
Нет живописи более поэтичней, чем живопись Боттичелли Сандро, и нет у великого Сандро картины более знаменитой, чем его “Венера”. Для Боттичелли его Венера – это воплощение идеи универсальной гармонии “золотого сечения”, господствующего в природе.
Пропорциональный анализ Венеры убеждает нас в этом .
А можно ли говорить о “золотом сечении” в музыке? Можно, если измерять музыкальное произведение по времени его исполнения. В музыка золотое сечение отражает особенности человеческого восприятия временных пропорций. Точка “золотого сечения” служит ориентиром формообразования. Часто на нее приходится кульминация. Это может быть так же самый яркий момент или самый тихий, или самое звуковысотное мест. (Прослушать фрагмент музыкального произведения.)
Таким образом, с помощью “золотого сечения” мы увидели родство между видами искусства: музыкой и архитектурой, живописью, математикой и литературой. (Сообщение “Слово о полку Игореве”.)
Сенсационное открытие сделал петербургский поэт и переводчик “Слова о полку Игореве” Андрей Чернов. Он нашел, что построение стихов загадочного древнерусского памятника подчиняется математическим законом. Исследования позволили сделать Чернову заключение о том, что в основу “Слова о полку Игореве”, состоящего из девяти песен, легла круговая композиция.
А поводом к тому, чтобы проверить гармонию поэму алгеброй, послужила статья о жизни древнегреческого математика Пифагора. Внимание Чернова привлекли рассуждения о “золотом сечени”и и о числе , которые восходят к Пифагору. Возникла неожиданная ассоциация: ведь в композиционном построении поэму тоже круг и, следовательно, должны быть “диаметр” и некая математическая закономерность.
Уже первые расчеты стали подтверждать закономерность, да еще какую! Если число стихов во всех трех частях (их 804) разделить на число стихов в первой и последней части (256), получается 3,14, т.е. число с точностью до третьего знака.
Открытие Чернова приводят к естественному вопросу: как древний автор “Слова о полку Игореве”, ничего не зная о числе , ни о других математических формулах, привнес организующее математическое начало в этот текст? Чернов предполагает, что автор использовал это интуитивно, подчиняясь образам древнегреческих архитектурных памятников. В те времена храм являл собой всеобъемлющий, художественный идеал, поэтому влиял на ритмику поэтического самовыражения.
Мы убедились, что все-таки существует связь между математикой и литературой, между архитектурой и музыкой. И это не случайно, ведь каждому искусству присуще стремление к стройности, соразмерности, гармонии. Природа совершенна, и у нее есть свои законы, выраженные с помощью математики и проявляющие во всех искусствах, независимо от того, литература это или математика. Эти свойства не выдуманы людьми. Они отражают свойства самой природы.
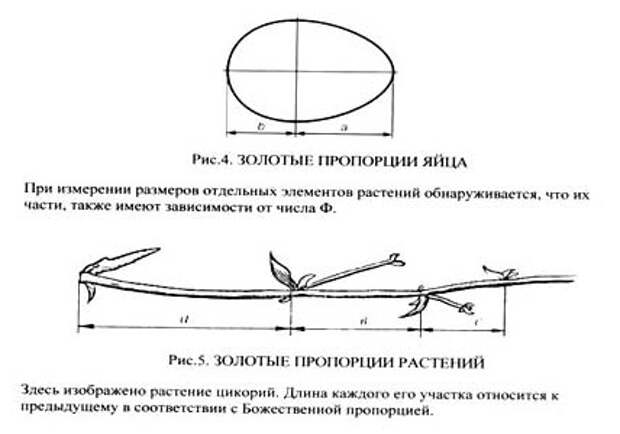
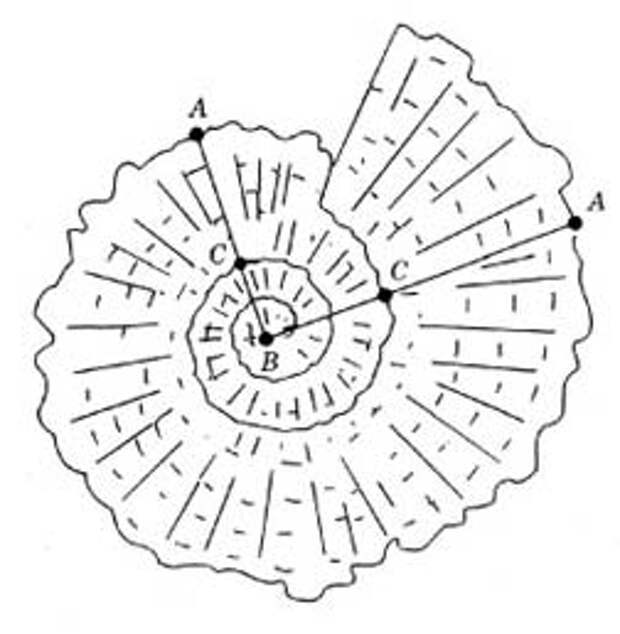
Если посмотреть на изображение раковины на нем точка С делит отрезок АВ приблизительно в золотом отношении.
“Золотое сечение” представляется тем моментом истины, без выполнения которого не возможно, вообще, что-либо сущее. Что бы мы ни взяли элементом исследования, “золотое сечение” будет везде; если даже нет видимого его соблюдения, то оно обязательно имеет место на энергетическом, молекулярном или клеточном уровнях.
Практическая работа
Работа проводится по группам. Каждой группе выдается чертеж или рисунок или фотография, где нужно найти золотое сечение.
Примеры изображений:
1.
2.
3. Чертеж. Фасад школьного здания.
Примечание от админа rustimes.com
Рекомендую книгу "Золотое сечение. Section divine"
(И.Ш.Шевелёв, М.А.Марутаев, И.Л.Шмелёв), Москва, Стройиздат, 1990.
http://rustimes.com/blog/post_1177437753.html
Категория: Книги Издание: Стройиздат, 1990
Золотое сечение (Section Divine)
Три взгляда на природу гармонии
Шевелев И.Ш., Марутаев М.А., Шмелев И.П.
Стройиздат, 1990
Аннотация:
Книга посвящена теоретическому обоснованию феномена золотого сечения, в котором авторы видят одну из универсальных закономерностей гармонии. Исследуются естественно-научное содержание понятий "гармония", "золотое сечение" и их проявления в архитектуре, музыке, психологии восприятия и формообразования живой природы, а также в таблице Менделеева, планетарных расстояниях, макро- и микрокосмосе и др. Многие проблемы поставлены и освещаются впервые.
Для архитекторов, музыкантов, искусствоведов, математиков, физиков, биологов, философов, а также всех, интересующихся проблемами гармонии.
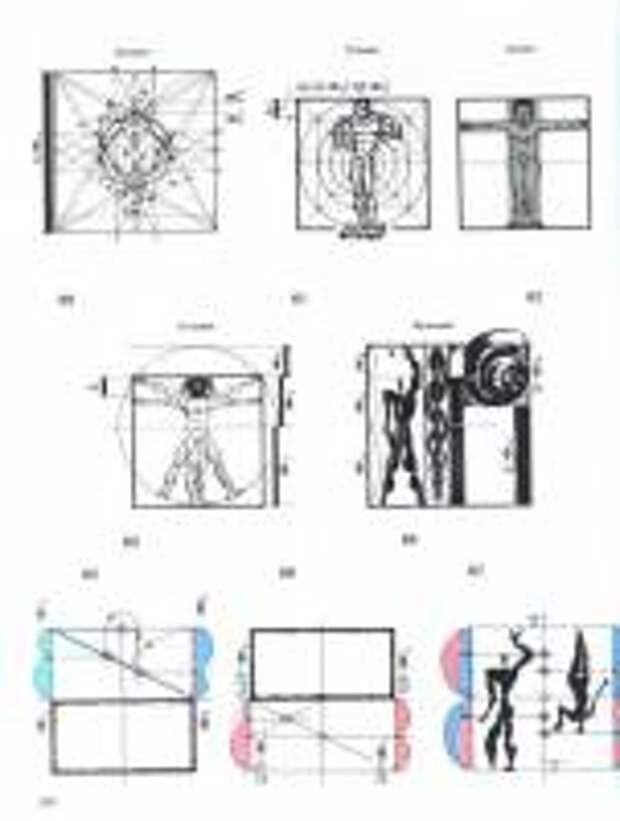
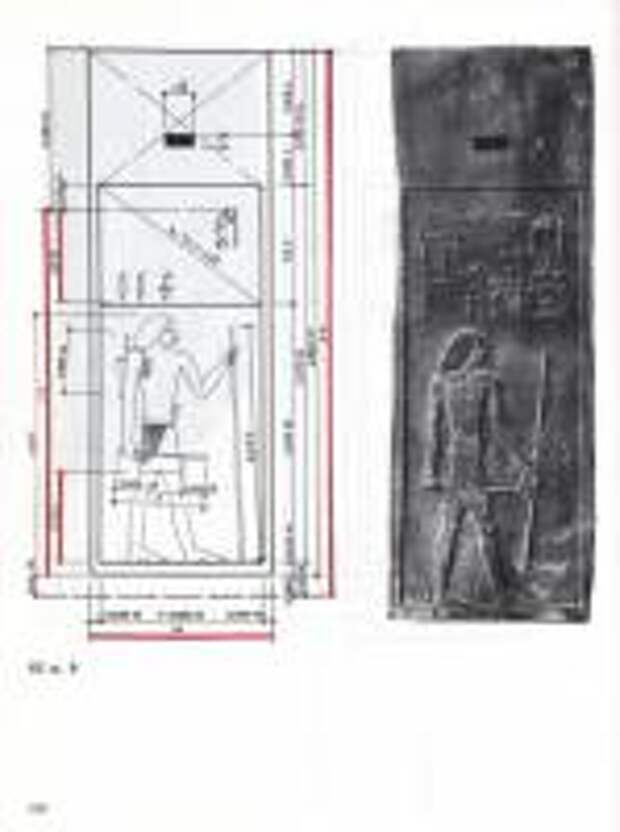
Примечание: Внимание! Тот PDF что можно скачать из сети БЕЗ некоторых страниц, а тот что мы публикуем - со всеми страницами.
PDF HQ (345 стр. Все страницы на месте) // Качество хорошее // 81,8 MB RAR
Скачать // Download
depositfiles.com - часть 1
depositfiles.com - часть 2
depositfiles.com - часть 3
Зеркало:
arch-grafika.ifolder.ru - часть 1
arch-grafika.ifolder.ru - часть 2
arch-grafika.ifolder.ru - часть 3
Золотое сечение в живописи - Ф. В. Ковалев читать онлайн
Свежие комментарии