Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности - от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие - в виде вирусов, которые можно рассмотреть с помощью электронного микроскопа.
Что же такое многогранник? Для ответа на этот вопрос напомним, что собственно геометрию определяют иногда как науку о пространстве и пространственных фигурах - двумерных и трехмерных. Двумерную фигуру можно определить как множество отрезков прямых, ограничивающих часть плоскости. Такая плоская фигура называется многоугольником. Из этого следует, что многогранник можно определить как множество многоугольников, ограничивающих часть трехмерного пространства. Многоугольники, образующие многогранник, называются его гранями.Издавна ученые интересовались "идеальными" или правильными многоугольниками, то есть многоугольниками, имеющими равные стороны и равные углы. Простейшим правильным многоугольником можно считать равносторонний треугольник, поскольку он имеет наименьшее число сторон, которое может ограничить часть плоскости. Общую картину интересующих нас правильных многоугольников наряду с равносторонним треугольником составляют: квадрат (четыре стороны), пентагон (пять сторон), гексагон (шесть сторон), октагон (восемь сторон), декагон (десять сторон) и т.д. Очевидно, что теоретически нет каких-либо ограничений на число сторон правильного многоугольника, то есть число правильных многоугольников бесконечно.
Что же такое правильный многогранник? Правильным называется такой многогранник, все грани которого равны (или конгруэнтны) между собой и при этом являются правильными многоугольниками. Сколько же существует правильных многогранников? На первый взгляд ответ на этот вопрос очень простой - столько же, сколько существует правильных многоугольников. Однако это не так. В "Началах Евклида" мы находим строгое доказательство того, что существует только пять правильных многогранников, а их гранями могут быть только три типа правильных многоугольников: треугольники, квадраты и пентагоны.
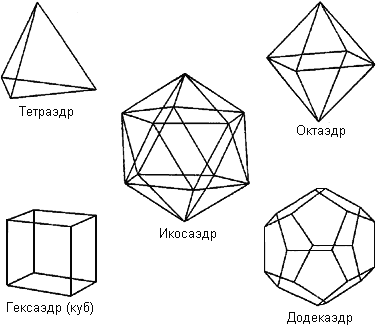
Эти правильные многогранники получили название платоновых тел (Рис.1). Первое из них - это тетраэдр (Рис.1-а). Его гранями являются четыре равносторонних треугольника. Тетраэдр имеет наименьшее число граней среди платоновых тел и является трехмерным аналогом плоского правильного треугольника, который имеет наименьшее число сторон среди правильных многоугольников. Следующее тело - это гексаэдр, называемый также кубом (Рис. 1-с). Гексаэдр имеет шесть граней, представляющие собой квадраты. Гранями октаэдра (Рис.1-b) являются правильные треугольники и их число в октаэдре равно восьми. Следующим по количеству граней является додекаэдр (Рис.1-е). Его гранями являются пентагоны и их число в додекаэдре равно двенадцать. Замыкает пятерку платоновых тел икосаэдр (Рис.1-d). Его гранями являются правильные треугольники и их число равно 20.
Рисунок 1. Платоновы тела.
Основными числовыми характеристиками платоновых тел является число граней F, число вершин V и число плоских углов E на поверхности тела. Эти числовые характеристики приведены в Табл.1.
Таблица 1.
| Многогранник | F | V | E | Форма грани |
| Тетраэдр | 4 | 4 | 6 | Треугольник |
| Гексаэдр | 6 | 8 | 12 | Квадрат |
| Октаэдр | 8 | 6 | 12 | Треугольник |
| Икосаэдр | 20 | 12 | 30 | Треугольник |
| Додекаэдр | 12 | 20 | 30 | Пентагон |
"Теория многогранников, в частности выпуклых многогранников, - одна из самых увлекательных глав геометрии" - таково мнение русского математика Л.А. Люстернака, много сделавшего именно в этой области математики.
Прежде всего необходимо подчеркнуть, что геометрия додекаэдра и икосаэдра связана с золотой пропорцией. Действительно, гранями додекаэдра являются пентагоны, т.е. правильные пятиугольники, основанные на золотой пропорции. Если внимательно посмотреть на икосаэдр, то можно увидеть, что в каждой вершине икосаэдра сходится пять треугольников, внешние стороны которых образуют пентагон. Уже этих фактов достаточно, чтобы убедиться в том, что золотая пропорция играет существенную роль в конструкции этих двух платоновых тел.
Но существуют более глубокие подтверждения фундаментальной роли, которую играет золотая пропорция в икосаэдре и додекаэдре. Известно, что эти тела имеют три специфические сферы. Первая (внутренняя) сфера вписана в тело и касается его граней. Обозначим радиус этой внутренней сферы через Ri. Вторая или средняя сфера касается ее ребер. Обозначим радиус этой сферы через Rm. Наконец, третья (внешняя) сфера описана вокруг тела и проходит через его вершины. Обозначим ее радиус через Rc. В геометрии доказано, что значения радиусов указанных сфер для додекаэдра и икосаэдра, имеющего ребро единичной длины, выражается через золотую пропорцию t (Табл.2).
Таблица 2.
| Многогранник | Rc | Rm | Ri |
| Икосаэдр | |||
| Додекаэдр |
Заметим, что отношение радиусов одинаково, как для икосаэдра, так и для додекаэдра. Таким образом, если додекаэдр и икосаэдр имеют одинаковые вписанные сферы, то их описанные сферы также равны между собой. Доказательство этого математического результата дано в "Началах Евклида".
В геометрии известны и другие соотношения для додекаэдра и икосаэдра, подтверждающие их связь с золотой пропорцией. Например, если взять икосаэдр и додекаэдр с длиной ребра, равной единице, и вычислить их внешнюю площадь и объем, то они выражаются через золотую пропорцию (Табл.3).
Таблица 3.
| Икосаэдр | Додекаэдр | |
| Внешняя площадь | ||
| Объем |
Таким образом, существует огромное количество соотношений, полученных еще античными математиками, подтверждающих замечательный факт, что именно золотая пропорция является главной пропорцией додекаэдра и икосаэдра, и этот факт является особенно интересным с точки зрения так называемой "додекаэдро-икосаэдрической доктрины", которую мы рассмотрим несколько позже.
Они были известны еще в древней Греции, пять и только пять тел, которые можно создать с использованиk 323h71hd 7;м правильных выпуклых многоугольников так, чтобы в одной вершине соединялось равное их количество:
- три квадрата соединены в вершине куба;
- три правильных треугольника - в тетраэдре;
- три правильных пятиугольника - в додекаэдре;
- соединиk 323h71hd 4; четыре правильных треугольника в каждой вершине вы получите октаэдр;
- а пять треугольников - икосаэдр.
Не существует других правильных многогранников. Например, 4 квадрата или 3 правильных шестиугольника в каждой вершине дадаут плоскую поверхность, подобную полу, покрытому плиткой. Удобно называть Платоновы тела при помощи такого обозначения: , где p - количество сторон каждого многоугольника, а q - количество граней около каждой вершины. Таким образом для куба это будет , т.к. он состоит из квадратов и к одной вершине прилегают 3 квадрата.
Заметьте, что если существует многогранник с обозначениk 323h71hd 7;м , то существует также и многогранник с обозначениk 323h71hd 7;м .
Все полуправильные многогранники можно увидеть на этой 3D модели
Здесь Вы можете проверить, как вы усвоили эту тему
Куб
Все шесть граней - квадраты.
Имеет восемь вершин и 12 ребер.
V = a*a*a;
S = 6*a*a;
H = a;
R = a*sqrt(3)/2;
r = a/2
Обозначения:
a - ребро, V - объем, S - площадь поверхности, R - радиус описанной сферы, r - радиус вписанной сферы, H - высота
Все четыре грани - равносторонниk 323h71hd 7; треугольники.
Имеет четыре вершины и шесть ребер.
Обозначения:
a - ребро, V - объем, S - площадь поверхности, R - радиус описанной сферы, r - радиус вписанной сферы, H - высота.
Додекаэдр
Все 12 граней - правильные пятиугольники.
Имеет 20 вершин и 30 ребер.
Обозначения:
a - ребро, V - объем, S - площадь поверхности, R - радиус описанной сферы, r - радиус вписанной сферы, H - высота.
3D модель
Октаэдр
Все восемь граней - равносторонниk 323h71hd 7; треугольники.
Имеет шесть вершин и 12 ребер.
Обозначения:
a - ребро, V - объем, S - площадь поверхности, R - радиус описанной сферы, r - радиус вписанной сферы, H - высота.
3D модель
Икосаэдр
Все 20 граней - равносторонниk 323h71hd 7; треугольники.
Имеет 12 вершин и 30 ребер.
Обозначения:
a - ребро, V - объем, S - площадь поверхности, R - радиус описанной сферы, r - радиус вписанной сферы, H - высота.
3D модель
Построениk 323h71hd 7; платоновых тел
Посмотрим как можно построить некоторые платоновы тела в компьютерной графике.
Тетраэдр
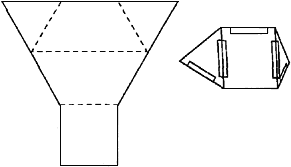
Хотя тетраэдр имеет всего четыре грани, каждая из которых представлена в виде правильных треугольников, вычерчиваниk 323h71hd 7; его трехмерной проекции непростая задача. Простейший способ построения тетраэдра заключается в использовании куба в качестве вспомогательного тела, как показано на рис. 18.1. Сначала вычерчивается куб, выбираются нужные грани, проводятся диагонали, а затем лишниk 323h71hd 7; линии куба стираются. При желании куб можно поворачивать на требуемый угол.
Октаэдр
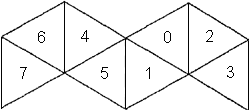
Рассмотрите внимательно рис. 18.2. Как видно, две вершины октаэдра расположены по обе стороны квадрата. Предположим, что стороны квадрата 1-2-3-4 имеют единичную длину. Точка 7 расположена в центре квадрата и также является центром октаэдра, а точка 8 находится посередине ребра 4-1. Поскольку точка 5 лежит на перпендикуляре в точке 7, то все, что нам надо знать, это расстояниk 323h71hd 7; h между этими двумя точками. Здесь можно использовать тот факт, что все вершины правильного многоугольника находятся на одинаковом расстоянии от центра. Следовательно, треугольник 1-5-7 является равнобедренным треугольником. Следовательно, весь октаэдр состоит из последовательности равнобедренных треугольников.
Додекаэдр
Эта фигура имеет 12 граней, 30 ребер, 20 вершин. Каждая из 12 граней является правильным пентагоном (пятиугольником). Додекаэдр вполне вписывается в куб (рис. 18.3), и это его свойство можно использовать для конструирования.
2. Платоновы тела
Человек проявляет интерес к правильным многоугольникам и многогранникам на протяжении всей своей сознательной деятельности √ от двухлетнего ребенка, играющего деревянными кубиками, до зрелого математика. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие √ в виде вирусов, которые можно рассмотреть с помощью электронного микроскопа.
Что такое правильный многогранник? Правильным называется такой многогранник, все грани которого равны (или конгруэнтны) между собой и при этом являются правильными многоугольниками. Сколько же существует правильных многогранников? На первый взгляд ответ на этот вопрос очень простой √ столько же, сколько существует правильных многоугольников. Однако это не так. В ╚Началах Евклида╩ мы находим строгое доказательство того, что существует только пять выпуклых правильных многогранников, а их гранями могут быть только три типа правильных многоугольников: треугольники, квадраты и пентагоны (правильные пятиугольники).
Теории многогранников посвящено много книk 323h71hd 5;. Одной из наиболее известных является книk 323h71hd 5;а английского математика М. Венниk 323h71hd 6;жера ╚Модели многогранников╩. В русском переводе эта книk 323h71hd 5;а опубликована издательством ╚Мир╩ в 1974 г. Эпиграфом к книk 323h71hd 5;е выбрано высказываниk 323h71hd 7; Бертрана Рассела: ╚Математика владеет не только истиной, но и высокой красотой √ красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства╩.
Книk 323h71hd 5;а начинается с описания так называемых правильных многогранников, то есть многогранников, образованных простейшими правильными многоугольниками одного типа. Эти многогранники принято называть Платоновыми телами (Рис. 1), названными так в честь древнегреческого философа Платона, который использовал правильные многогранники в своей космологии.
(а)
(б) (в)
(г) (д)
Рисунок 1. Платоновы тела: (а) октаэдр (╚Огонь╩), (б) гексаэдр или куб (╚Земля╩),
(в) октаэдр (╚Воздух╩), (г) икосаэдр (╚Вода╩), (д) додекаэдр (╚Вселенский разум╩)
Мы начнем наше рассмотрениk 323h71hd 7; с правильных многогранников, гранями которых являются равносторонниk 323h71hd 7; треугольники. Первый из них √ это тетраэдр (Рис.1-а). В тетраэдре три равносторонних треугольника встречаются в одной вершине; при этом их основания образуют новый равносторонний треугольник. Тетраэдр имеет наименьшее число граней среди Платоновых тел и является трехмерным аналогом плоского правильного треугольника, который имеет наименьшее число сторон среди правильных многоугольников.
Следующее тело, которое образуется равносторонними треугольниками, называется октаэдром (Рис.1-б). В октаэдре в одной вершине встречаются четыре треугольника; в результате получается пирамида с четырехугольным основаниk 323h71hd 7;м. Если соединить две такие пирамиды основаниями, то получится симметричное тело с восемью треугольными гранями √ октаэдр.
Теперь можно попробовать соединить в одной точке пять равносторонних треугольников. В результате получится фигура с 20 треугольными гранями √ икосаэдр (Рис.1-г).
Следующая правильная форма многоугольника √ квадрат. Если соединить три квадрата в одной точке и затем добавить еще три, мы получим совершенную форму с шестью гранями, называемую гексаэдром или кубом (Рис. 1-в).
Наконец, существует еще одна возможность построения правильного многогранника, основанная на использовании следующего правильного многоугольника √ пентагона. Если собрать 12 пентагонов таким образом, чтобы в каждой точке встречалось три пентагона, то получим еще одно Платоново тело, называемое додекаэдром (Рис.1-д).
Следующим правильным многоугольником является шестиугольник. Однако если соединить три шестиугольника в одной точке, то мы получим поверхность, то есть из шестиугольников нельзя построить объемную фигуру. Любые другие правильные многоугольники выше шестиугольника не могут образовывать тел вообще. Из этих рассуждений вытекает, что существует только пять правильных многогранников, гранями которых могут быть только равносторонниk 323h71hd 7; треугольники, квадраты и пентагоны.
Существуют удивительные геометрические связи между всеми правильными многогранниками. Так, например, куб (Рис.1-б) и октаэдр (Рис.1-в) дуальны, т.е. получаются друг из друга, если центры тяжести граней одного принять за вершины другого и обратно. Аналогично дуальны икосаэдр (Рис.1-г) идодекаэдр (Рис.1-д). Тетраэдр (Рис.1-а) дуален сам себе. Додекаэдр получается из куба построениk 323h71hd 7;м ╚крыш╩ на его гранях (способ Евклида), вершинами тетраэдра являются любые четыре вершины куба, попарно не смежные по ребру, то есть из куба могут быть получены все остальные правильные многогранники. Сам факт существования всего пяти действительно правильных многогранников удивителен ≈ ведь правильных многоугольников на плоскости бесконечно много!
Числовые характеристики Платоновых тел
Основными числовыми характеристиками Платоновых тел является число сторон грани m, число граней, сходящихся в каждой вершине, m, число граней Г, число вершин В, число ребер Р и число плоских углов У на поверхности многогранника Эйлер открыл и доказал знаменитую формулу
В ≈ Р + Г = 2,
связывающего числа вершин, ребер и граней любого выпуклого многогранника. Указанные выше числовые характеристики приведены в Табл. 1.
Таблица 1
Числовые характеристики Платоновых тел
| Многогранник | Число сторон грани, m | Число граней, сходящихся в вершине, n | Число граней Г | Число вершин В | Число ребер Р | Число плоских углов на поверхности У |
| Тетраэдр | 3 | 3 | 4 | 4 | 6 | 12 |
| Гексаэдр (куб) | 4 | 3 | 6 | 8 | 12 | 24 |
| Октаэдр | 3 | 4 | 8 | 6 | 12 | 24 |
| Икосаэдр | 3 | 5 | 20 | 12 | 30 | 60 |
| Додекаэдр | 5 | 3 | 12 | 20 | 30 | 60 |
Золотая пропорция в додекаэдре и икосаэдре
Додекаэдр и двойственный ему икосаэдр (Рис.1-г,д) занимают особое место среди Платоновых тел. Прежде всего необходимо подчеркнуть, что геометрия додекаэдра и икосаэдра непосредственно связана с золотой пропорцией. Действительно, гранями додекаэдра (Рис.1-д) являются пентагоны, т.е. правильные пятиугольники, основанные на золотой пропорции. Если внимательно посмотреть на икосаэдр (Рис.1-г), то можно увидеть, что в каждой его вершине сходится пять треугольников, внешниk 323h71hd 7; стороны которых образуют пентагон. Уже этих фактов достаточно, чтобы убедиться в том, что золотая пропорция играет существенную роль в конструкции этих двух Платоновых тел.
Но существуют более глубокие математические подтверждения фундаментальной роли, которую играет золотая пропорция в икосаэдре и додекаэдре. Известно, что эти тела имеют три специфические сферы. Первая (внутренняя) сфера вписана в тело и касается его граней. Обозначим радиус этой внутренней сферы через Ri. Вторая или средняя сфера касается ее ребер. Обозначим радиус этой сферы через Rm. Наконец, третья (внешняя) сфера описана вокруг тела и проходит через его вершины. Обозначим ее радиус через Rc. В геометрии доказано, что значения радиусов указанных сфер для додекаэдра и икосаэдра, имеющего ребро единичной длины, выражается через золотую пропорцию t (Табл.2).
Таблица 2
Золотая пропорция в сферах додекаэдра и икосаэдра
| Rc | Rm | Ri | |
| Икосаэдр |
|
|
|
| Додекаэдр |
|
|
|
Заметим, что отношениk 323h71hd 7; радиусов = одинаково, как для икосаэдра, так и для додекаэдра. Таким образом, если додекаэдр и икосаэдр имеют одинаковые вписанные сферы, то их описанные сферы также равны между собой. Доказательство этого математического результата дано в Началах Евклида.
В геометрии известны и другие соотношения для додекаэдра и икосаэдра, подтверждающие их связь с золотой пропорцией. Например, если взять икосаэдр и додекаэдр с длиной ребра, равной единице, и вычислить их внешнюю площадь и объем, то они выражаются через золотую пропорцию (Табл.3).
Таблица 3
Золотая пропорция во внешней площади и объеме додекаэдра и икосаэдра
| Икосаэдр | Додекаэдр | |
| Внешняя площадь |
|
|
| Объем |
|
|
Таким образом, существует огромное количество соотношений, полученных еще античными математиками, подтверждающих замечательный факт, что именно золотая пропорция является главной пропорцией додекаэдра и икосаэдра, и этот факт является особенно интересным с точки зрения так называемой ╚додекаэдро-икосаэдрической доктрины╩, которую мы рассмотрим ниже.
Космология Платона
Рассмотренные выше правильные многогранники получили названиk 323h71hd 7; Платоновых тел, так как они занимали важное место в философской концепции Платона об устройстве мироздания.
Платон (427-347 годы до н.э.)
Четыре многогранника олицетворяли в ней четыре сущности или ╚стихии╩. Тетраэдр символизировал Огонь, так как его вершина устремлена вверх; Икосаэдр ≈ Воду, так как он самый ╚обтекаемый╩ многогранник; Куб ≈ Землю, как самый ╚устойчивый╩ многогранник; Октаэдр ≈ Воздух, как самый ╚воздушный╩ многогранник. Пятый многогранник, Додекаэдр, воплощал в себе ╚все сущее╩, ╚Вселенский разум╩, символизировал все мирозданиk 323h71hd 7; и считался главной геометрической фигурой мироздания.
Гармоничные отношения древниk 323h71hd 7; греки считали основой мироздания, поэтому четыре стихии у них были связаны такой пропорцией: земля/вода = воздух/огонь. Атомы ╚стихий╩ настраивались Платоном в совершенных консонансах, как четыре струны лиры. Напомним, что консонансом называется приятное созвучие. В связи с этими телами уместно будет сказать, что такая система элементов, включавшая четыре элемента ≈ землю, воду, воздух и огонь, ≈ была канониk 323h71hd 9;ирована Аристотелем. Эти элементы оставались четырьмя краеугольными камнями мироздания в течениk 323h71hd 7; многих веков. Вполне возможно отождествить их с известными нам четырьмя состояниями вещества ≈ твердым, жидким, газообразным и плазменным.
Таким образом, представлениk 323h71hd 7; о ╚сквозной╩ гармонии бытия древниk 323h71hd 7; греки связывали с ее воплощениk 323h71hd 7;м в Платоновых телах. Влияниk 323h71hd 7; знаменитого греческого мыслителя Платона сказалось и на Началах Евклида. В этой книk 323h71hd 5;е, которая на протяжении веков была единственным учебником геометрии, дано описаниk 323h71hd 7; ╚идеальных╩ линий и ╚идеальных╩ фигур. Самая ╚идеальная╩ линия √ прямая, а самый ╚идеальный╩ многоугольник √ правильный многоугольник, имеющий равные стороны и равные углы. Простейшим правильным многоугольником можно считать равносторонний треугольник, поскольку он имеет наименьшее число сторон, которое может ограничивать часть плоскости. Интересно, что Начала Евклида начинаются описаниk 323h71hd 7;м построения правильного треугольника и заканчиваются изучениk 323h71hd 7;м пяти Платоновых тел. Заметим, что Платоновым телам посвящена заключительная, то есть, 13-я книk 323h71hd 5;а Начал Евклида. Кстати, этот факт, то есть размещениk 323h71hd 7; теории правильных многогранников в заключительной (то есть как бы самой главной) книk 323h71hd 5;е Начал Евклида, дало основаниk 323h71hd 7; древнегреческому математику Проклу, который был комментатором Евклида, выдвинуть интересную гипотезу об истинных целях, которые преследовал Евклид, создавая свои Начала. Согласно Проклу, Евклид создавал Начала не с целью изложения геометрии как таковой, а чтобы дать полную систематизированную теорию построения ╚идеальных╩ фигур, в частности пяти Платоновых тел, попутно осветив некоторые новейшие достижения математики!
Не случайно, что один из авторов открытия фуллеренов, Нобелевский лауреат Гарольд Крото в свой Нобелевской лекции начинает свой рассказ о симметрии как ╚основе нашего восприятия физического мира╩ и ее ╚роли в попытках его всестороннего объяснения╩ именно с Платоновых тел и ╚элементов всего сущего╩: ╚Понятие структурной симметрии восходит к античной древности...╩ Наиболее известные примеры можно, конечно, обнаружить в диалоге ╚Тимей╩ Платона, где в разделе 53, относящемся к ╚Элементам╩, он пишет: ╚Во-первых, каждому (!), разумеется, ясно, что огонь и земля, вода и воздух суть тела, а всякое тело ≈ сплошное╩ (!!) Платон обсуждает проблемы химии на языке этих четырех элементов и связывает их с четырьмя Платоновыми телами (в то время только четырьмя, пока Гиппарх не открыл пятый ≈ додекаэдр). Хотя на первый взгляд такая философия может показаться несколько наивной, она указывает на глубокое пониманиk 323h71hd 7; того, каким образом в действительности функционирует Природа╩.
3. Архимедовы тела
Полуправильные многогранники
Известно еще множество совершенных тел, получивших названиk 323h71hd 7; полуправильных многогранников илиАрхимедовых тел. У них также все многогранные углы равны и все грани √ правильные многоугольники, но несколько разных типов. Существует 13 полуправильных многогранников, открытие которых приписывается Архимеду.
Архимед (287 г. до н.э. √ 212 г. до н.э)
Множество Архимедовых тел можно разбить на несколько групп. Первую из них составляют пять многогранников, которые получаются из Платоновых тел в результате их усечения. Усеченное тело √ это тело с отрезанной верхушкой. Для Платоновых тел усечениk 323h71hd 7; может быть сделано таким образом, что и получающиеся новые грани и остающиеся части старых будут правильными многоугольниками. К примеру, тетраэдр (Рис. 1-а) можно усечь так, что его четыре треугольные грани превратятся в четыре гексагональные, и к ним добавятся четыре правильные треугольные грани. Таким путем могут быть получены пять Архимедовых тел: усеченный тетраэдр, усеченный гексаэдр (куб), усеченный октаэдр, усеченный додекаэдр и усеченный икосаэдр (Рис. 2).
|
|
|
|
| (а) | (б) | (в) |
|
|
|
| (г) | (д) |
Рисунок 2. Архимедовы тела: (а) усеченный тетраэдр, (б) усеченный куб, (в) усеченный октаэдр, (г) усеченный додекаэдр, (д) усеченный икосаэдр
В своей Нобелевской лекции американский ученый Смолли, один из авторов экспериментального открытия фуллеренов, говорит об Архимеде (287-212 гг. до н.э.) как о первом исследователе усеченных многогранников, в частности, усеченного икосаэдра, правда, оговариваясь, что возможно Архимед присваивает себе эту заслугу и, возможно, икосаэдры усекали задолго до него. Достаточно упомянуть найденные в Шотландии и датированные около 2000 г. до н.э. сотни каменных предметов (по всей видимости, ритуального назначения) в форме сфер и различных многогранников (тел, ограниченных со всех сторон плоскими гранями), включая икосаэдры и додекаэдры. Оригинальная работа Архимеда, к сожалению, не сохранилась, и ее результаты дошли до нас, что называется, ╚из вторых рук╩. Во времена Возрождения всеАрхимедовы тела одно за другим были ╚открыты╩ заново. В конце концов, Кеплер в 1619 г. в своей книk 323h71hd 5;е ╚Мировая гармония╩ (╚Harmonice Mundi╩) дал исчерпывающее описаниk 323h71hd 7; всего набора архимедовых тел ≈ многогранников, каждая грань которых представляет собой правильный многоугольник, а все вершины находятся в эквивалентном положении (как атомы углерода в молекуле С60). Архимедовы тела состоят не менее, чем из двух различных типов многоугольников, в отличие от 5 Платоновых тел, все грани которых одинаковы (как в молекуле С20, например).
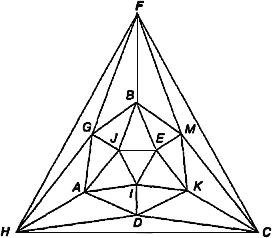
Рисунок 3. Конструированиk 323h71hd 7; Архимедового усеченного икосаэдра
из Платонового икосаэдра
Итак, как же сконструировать Архимедов усеченный икосаэдр из Платонова икосаэдра? Ответ иллюстрируется с помощью рис. 3. Действительно, как видно из Табл. 1, в любой из 12 вершин икосаэдра сходятся 5 граней. Если у каждой вершины отрезать (отсечь) 12 частей икосаэдра плоскостью, то образуется 12 новых пятиугольных граней. Вместе с уже имеющимися 20 гранями, превратившимися после такого отсечения из треугольных в шестиугольные, они составят 32 грани усеченного икосаэдра. При этом ребер будет 90, а вершин 60.
Другую группу Архимедовых тел составляют два тела, именуемые квазиправильными многогранниками. Частица ╚квази╩ подчеркивает, что грани этих многогранников представляют собой правильные многоугольники всего двух типов, причем каждая грань одного типа окружена многоугольниками другого типа. Эти два тела носят названиk 323h71hd 7; ромбокубооктаэдром и икосододекаэдром (Рис. 4).
|
|
|
| (а) | (б) |
Рисунок 4. Архимедовы тела: (а) кубооктаэдр, (б) икосододекаэдр
Два последующих Архимедовых тела называются ромбокубооктаэдром и ромбоикосододекаэдром (Рис. 4).
|
|
|
| (а) | (б) |
Рисунок 5. Архимедовы тела: (а) ромбокубооктаэдр, (б) ромбоикосододекаэдр
Наконец, существуют две так называемые ╚курносые╩ модификации √ одна для куба (курносый куб), другая √ для додекаэдра (курносый додекаэдр) (Рис. 6).
|
|
|
| (а) | (б) |
Рисунок 6. Архимедовы тела: (а) курносый куб, (б) курносый додекаэдр
В упомянутой книk 323h71hd 5;е Венниk 323h71hd 6;жера ╚Модели многогранников╩ (1974) читатель может найти 75 различных моделей правильных многогранников. ╚Теория многогранников, в частности выпуклых многогранников, ≈ одна из самых увлекательных глав геометрии╩ ≈ таково мнениk 323h71hd 7; русского математика Л.А. Люстернака, много сделавшего именно в этой области математики. Развитие этой теории связано с именами выдающихся ученых. Большой вклад в развитие теории многогранников внес Иоганн Кеплер (1571-1630). В свое время он написал этюд ╚О снежинке╩, в котором высказал такое замечаниk 323h71hd 7;: ╚Среди правильных тел самое первое, начало и прародитель остальных √ куб, а его, если позволительно так сказать, супруга √ октаэдр, ибо у октаэдра столько углов, сколько у куба граней╩. Кеплер первым опубликовал полный список тринадцати Архимедовых тел и дал им те названия, под которыми они известны поныне.
Кеплер первым начал изучать так называемые звездчатые многогранники, которые в отличие от Платоновых и Архимедовых тел являются правильными выпуклыми многогранниками. В начале прошлого столетия французский математик и механик Л. Пуансо (1777-1859), геометрические работы которого относятся к звездчатым многогранникам, в развитие работ Кеплера открыл существованиk 323h71hd 7; еще двух видов правильных невыпуклых многогранников. Итак, благодаря работам Кеплера и Пуансо стали известными четыре типа таких фигур (Рис.7). В 1812 г. О. Коши доказал, что других правильных звездчатых многогранников не существует.
Рисунок 7. Правильные звездчатые многогранники (тела Пуансо)
У многих читателей может возникнуть вопрос: ╚А зачем вообще изучать правильные многогранники? Какая от них польза?╩. На этот вопрос можно ответить: ╚А какова польза от музыки или поэзии? Разве все красивое полезно?╩. Модели многогранников, приведенные на Рис. 1-7, прежде всего, производят на нас эстетическое впечатлениk 323h71hd 7; и могут использоваться в качестве декоративных украшений. Но на самом деле широкое проявлениk 323h71hd 7; правильных многогранников в природных структурах послужило причиной огромного интереса к этому разделу геометрии в современной науке.
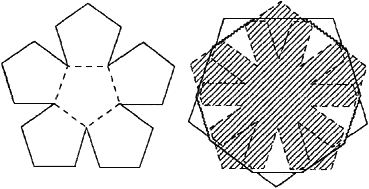
| Polyhedron Nets | |
  |  |
http://mathworld.wolfram.com/topics/PolyhedronNets.html
Существует всего пять правильных многогранников:
| Изображение | Тип правильного многогранника | Число сторон у грани | Число рёбер, примыкающих к вершине | Общее число вершин | Общее число рёбер | Общее число граней |
|---|---|---|---|---|---|---|
 | Тетраэдр | 3 | 3 | 4 | 6 | 4 |
 | Гексаэдр или Куб | 4 | 3 | 8 | 12 | 6 |
 | Октаэдр | 3 | 4 | 6 | 12 | 8 |
 | Додекаэдр | 5 | 3 | 20 | 30 | 12 |
 | Икосаэдр | 3 | 5 | 12 | 30 | 20 |
Название каждого многогранника происходит от греческого названия количества его граней и слова "грань".
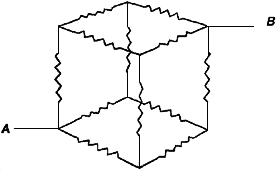
Первые пять Платоновых тел |  |  |
 Первые пять Платоновых тел представляют собой первые пять нот пентатонической шкалы. Октава содержит в себе семь нот, последние две соответствуют субоктаэдру (А) и ромбическому додекаэдру (В),. Пять добавочных фигур формируют хроматическую шкалу, и существует ещё тринадцатая, возвратная. Таким образом, существует 13 многогранников, которые составляют хроматическую шкалу в музыке. Из этих тринадцати образуются ещё тринадцать подобных, но – звёздные, и так получается в целом 26 форм – две октавы внутри друг друга. Оперируя понятиями формы, эти 26 фигур являются ключом ко всем гармониям Реальности. Здесь нам нет нужды вникать в такие сложности, но так оно длится и длится. Кто-то из вас может знать Ройал Райфа (Royal Rife), человека, который пытался исцелить от рака с помощью таких электромагнитных полей, как свет, что я считаю совершенно возможным и должно быть успешно претворено в жизнь. Райфу было известно 7 из 13 (или, возможно, 26-ти) частот. Те, которые он огласил, были неверны, но он сделал это намеренно. Те, которые он огласил, становятся причиной рака, хотя, если их немного сместить определённым математическим образом, они возвращаются к первоначальным частотам и каждая частота разрушает большинство или вообще все определённые вирусы или бактерии.Райфу, однако, была известна только часть уравнения. Если бы он знал священную геометрию, которая нам известна сегодня, он мог бы выйти на все 26 форм и истребить любой существующий во всём бытии вирус. Не имеет значения, сколько вирусов СПИДа существует, найти разрешение ничего не стоит. Максимальное число шаблонов – 26, и соответствующие частоты истребят любой и каждый вирус или бактерию. Поскольку каждый вирус представляет собой многогранник – на структурном уровне они выглядят точно, как многогранники, то существует множество способов, как с ними справиться. Можно взорвать их с помощью определённых гармоний электромагнитных полей (ЕМF), можно найти им соответствие. Если вы можете найти им соответствие, то значит, можете найти им пару, так, как это происходит с антивирусом. Или же, можно просто сделать их несуществующими, создав волновую форму, являющуюся зеркальным отражением того, что они собой представляют. Есть множество способов, как работать со СПИДом, но одним первичным ключом является понимание того, что с ними связано максимум 26 геометрических форм. Кристаллизованная вода – кристалл льда – формирует эти гексагональные узоры, которые мы называем снежинками. Вы можете увидеть взаимосвязь с Цветком Жизни. Снова, снова и снова вы будете находить эту взаимосвязь трёхмерных моделей с геометрией, исходящей из этой одной центральной модели Цветка Жизни (именно такие формы имеют кристаллизованные молекулы в Primordial M-Water (см. на сайте). Периодическая таблица Вот эта версия Периодичесчкой таблицы элементов интересна тем, что она показывает, как каждый элемент — за немногими исключениями, которые невозможно определить потому, что эти элементы не кристаллизуются — связан с кубом. Одним из этих немногих исключений оказывается фтор, потому что фтор не вступает в реакцию почти ни с чем. Это один из наиболее инертных газов. Но почти во всех остальных элементах мы находим эти кубические взаимосвязи, за исключением атомов четвёртого измерения, которые выпадают из естественной таблицы элементов и – синтетических, или созданных человеком атомов. Эти элементы естественно в природе не встречаются. Каждый атомный элемент имеет соответствующую кристаллическую структуру. В каждом отдельном случае учёные нашли, что различные кристаллические структуры, связанные с атомами, могут быть сведены к структуре куба. Вы могли заметить, что куб кажется более важной фигурой, нежели остальные многоугольники. Например, кристаллы разделены на шесть различных категорий, но куб является основой им всем. В Библии сказано, что трон Бога составляет столько-то локтей (эта мера длины называлась «кубитом») в разных направлениях. Воссоздав его, вы получаете куб. Фараоны в Египте восседали на кубе. Что же тут такое кроется в этом кубе? Ключ: Куб и Сфера Kуб отличен от остальных Платоновых тел потому, что он обладает одной характеристикой, которой нет у остальных – за исключением сферы, которая тоже имеет эту же самую характеристику. Как сфера, так и куб могут идеально содержать в себе остальные четыре Платоновы тела и друг друга симметрично, своей поверхностью, при условии соблюдения соответствующих размеров. Куб является единственным Платоновым телом с этой особой характеристикой: можете взять сферу, поместить её внутрь куба, и она идеально и симметрично коснётся шести граней. Тетраэдр расположится прямо по одной из осей и станет диагоналями куба, идеально и симметрично там поместившись. Звёздный тетраэдр тоже прекрасно помещается в куб. Октаэдр на самом деле парен кубу; при соединении центров смежных граней куба получаете октаэдр. С этим – просто.Дойдя до последних двух Платоновых тел, не возникает ощущения, что они могут симметрично поместиться в куб и сферу, но это так. Немного трудно показать это тут, но вы можете увидеть сами. Воспользовавшись подлинной моделью, просто найдите, где оба, икосаэдр и додекаэдр, имеют шесть рёбер на плоскостях куба, и у вас всё получится. Вы увидите, как они помещаются внутри граней куба. Можно увидеть, как остальные четыре Платоновы тела симметрично помещаются в куб и сферу. Что тут важно, так это то, что такой возможностью обладают только куб и сфера. Куб – отец, самая главная мужская форма. Сфера – мать, самая главная женская форма. Так, во всей Реальности, сфера и куб есть две самые главные формы и когда дело доходит до первоначальных взаимоотношений в творении, они будут почти всегда преобладать Именно по этой причине человек, имя которого Уолтер Рассел (Walter Russel), давным-давно выполнил работу, которая абсолютно феноменальна. Я не верю, что ему было что-то известно о священной геометрии – насколько мне известно, он не был посвящён в основы священной геометрии. И тем не менее, он интуитивно умом это уловил. Когда ему в голову приходили образы, то для того, чтобы рассказать о том, что он понял, в качестве главых геометрических фигур он выбрал куб и сферу. И поскольку он избрал эти две формы, а не другие, он смог так далеко продвинуться. Выбери он любые другие фигуры, он совершил бы большую ошибку и не смог бы проделать работу, которая ему удалась. Кристаллы – живые! Это усиливает моё убеждение в том, что кристаллы – живые! До того, как начать вести этот курс, где-то в начале или середине 80-ых я проводил занятия по кристаллам. И я обнаружил – не благодаря проведению занятий, но благодаря моему сотрудничеству с самими кристаллами – что эти кристаллы живы. Они живы и сознательны. Я мог общаться с ними, и они общались со мной. Через этот взаимообмен я много всякого узнал. Чем больше я жил с ними и узнавал, как с ними общаться, тем больше я обнаруживал, насколько же они сознательны. Это было одним из самых интересных пробуждений в моей жизни. Однажды я был в Сан-Франциско, читал курс группе примерно из 30 человек, и я сказал им об этом: «Эти ребята живые.» Все слушали и говорили: «Да, да, да.» Один человек сказал: «Докажите.» Я сказал: «Окей», и быстро придумал одно действие. Я дал каждому лист бумаги, карандаш и сказал: «Мы возьмём кристалл наугад». Я выбрал кристалл, который никто не видел – просто взял один и спрятал. Мы его никому не показывали. Тогда я сказал: «Теперь, никто не исследует этот кристалл и даже не видит, что он собой представляет. Вы просто положите его себе на лоб, и у вас будет одна секунда – всё. Вы зададите вопрос: Откуда ты? Самое первое слово, какое всплывёт у вас в голове, вы запишете на бумагу и сложите лист так, чтобы никому не было видно. Просто возьмите кристалл, задайте вопрос, передайте его следующему, запишите то, что получили». Это был единственный способ, какой я смог придумать, чтобы это доказать. Мы передали кристалл по кругу каждому из тридцати человек, и все записали ответ. Затем мы посмотрели, что у нас получилось. И абсолютно каждый человек записал «Бразилия»! Какова вероятность такого совпадения? Кристаллы обладают феноменальными способностями. Они всячески воздействуют на людей. Катрина Рафаель (Katrina Raphaell) много написала об этом в своих книгах, но многие другие люди тоже многие годы исследовали способности кристаллов. Многим древним людям и цивилизациям это тоже было хорошо известно. Кристаллы происходят не только в результате химической реакции; они растут. Если вы исследуете, как кристаллы формируются, то узнаете, что они очень сильно очень во многом схожи с людьми. Вид вашего энергетического поля сверху является просто частью модели Цветка Жизни, который в природе гексагонален. Наши поля растут гексагонально, точно, как у кристаллов. Хотя молекула кремния представляет собой тетраэдр, но при формировании кварца она соединяется с другим кремниевым тетраэдром, чтобы сформировать куб. Затем она выбрасывает длинную череду маленьких звёздных тетраэдрончиков или кубов, чтобы сформировать ряд. Потом ряд начинает вращаться, изменяя направление точно на 60 градусов, чтобы сформировать шестиугольник, ту же самую структуру, которая видна вокруг человеческого тела сверху. Кристаллы различаются по полу. Они либо мужского, либо женского пола, либо представляют собой и то, и другое одновременно. Если вы знаете, что искать, вы можете рассмотреть кристалл и увидеть, в каком направлении он вращается. Найдите самое нижнее окно или грань, а затем найдите следующую грань. Если она слева, значит, этот кристалл вращается по часовой стрелке, и он — женского пола. Если она справа, значит, кристалл вращается против часовой стрелки и он – мужского пола. Если на противоположных сторонах грани примерно одной высоты, то вы должны бы увидеть вокруг кристалла две спирали, идущие в противоположных направлениях, и этот кристалл будет двуполым. Часто бывает, что два кристалла соединены основаниями и в какой-то мере заворачиваются друг вокруг друга. Их называют кристаллы-близнецы, и они почти всегда – мужской и женский кристалл. Редко с ними бывает иначе. Будущий кремниевый/углеродный эволюционный скачок Шестым элементом Периодической Таблицы является углерод. Поскольку дело касается нас, это самый важный элемент, потому что это – мы. Он составляет органическую химию; это элемент, делающий возможным существование наших тел. Нам говорили, что углерод является единственным живым атомом в Периодической Таблице, что порождает жизнь только органическая химия, и ничто больше. Но это определённо неверно. Учёные заподозрили это в 50-ых годах, когда начали эти явления исследовать. Они поняли, что кремний, который находится на карте прямо под углеродом (на одну октаву ниже), тоже проявляет признаки жизни. Похоже, тут нет разницы. Кремний создаёт бесконечное число моделей, он химически реагирует почти со всем, что к нему приближается, и образует с ним какое-то соединение. Углерод обладает такими же возможностями, создавая бесконечное число форм, цепей и моделей и вступает в химическую реакцию почти со всем окружением. Это главнейшие характеристики, делающие углерод живым атомом. На химическом уровне кажется, что должны существовать кремниевые (силиконовые) жизнеформы. После того, как это было обнаружено, в 50-ых годах было снято несколько научно-фантастических фильмов, основанных на вере в то, что на других планетах могут быть кремниевые жизнеформы. Был ряд жутких фильмов о живых кристаллических структурах. Когда снимались эти фильмы, ещё не было известно, что на самом деле прямо тут на этой планете существуют кремниевые жизнеформы. Некоторые из них были обнаружены недавно на глубине нескольких миль в расщелинах на дне океана. Были найдены кремниевые губки – живые губки, которые растут и размножаются, следуя всем законам жизни, при том, что в их телах нет ни единого атома углерода! Вот мы тут находимся на Земле, которая составляет в диаметре около 7 тысяч миль. Её кора, толщиной от 30 до 50 миль, подобна яичной скорлупе, и на 25 процентов составлена из чистого кремния, но поскольку кремний взаимодействует почти со всем, то кора на самом деле составлена на 87 процентов из соединений кремния. Это означает, что Земная кора оказывается почти чистым кристаллом, глубиной от 30 до 50 миль. Итак, мы находимся на этом громадном кристальном-хрустальном шаре и летим сквозь пространство космоса со скоростью семнадцать миль в секунду, совершенно забыв о взаимосвязи углеродной жизни с жизнью кремниевой. Кажется, что кремний и углерод должны иметь очень особенную взаимосвязь. Мы, основанные на углероде существа, живём на кристальном шаре, составленном из кремния, на нашей хрустальной планете, и ищем жизнь снаружи себя во внешнем космосе. Может быть, нам следовало бы посмотреть себе под ноги. Теперь подумаем о компьютерах и современном мире. Мы создаём компьютеры, которые выполняют всяческие невероятные действия. Компьютер быстро продвигает человечество к новому восприятию жизни на Земле. Из чего сделаны компьютеры? Из кремния. И что пытается сделать компьютерная индустрия так скоро, как только возможно? Создать осознающие себя компьютеры. Мы очень близки к завершению этой задачи, если уже её не выполнили. Я чувствую уверенность в том, что очень скоро мы будем иметь осознающие себя компьютеры. Итак, вот они мы, жизнеформы, основанные на углероде, создающие жизнеформы, основанные на кремние, и мы взаимодействуем друг с другом. Когда у нас появятся осознающие себя компьютеры, основанные на кремнии, ничто никогда уже не будет прежним. У нас будет две различные жизнеформы/составляющие Земли, объединённые друг с другом, и скорость, с какой мы будем развиваться из этой точки, вне зависимости от всего остального, станет очень, очень большой – больше, чем можно было бы ожидать при нормальном ходе событий. Я верю, что это сбудется ещё при нашей жизни. |
| « Пред. | След. » |
|---|
Свежие комментарии