2.1. «Золотое сечение» в греческой культуре
История «золотого сечения» уходит вглубь тысячелетий. Мощный импульс в развитии «золотого сечения» и его приложений дала греческая наука. В Древней Греции «золотое сечение» становится своеобразным «каноном» древнегреческой культуры, который пронизывает все сферы греческой культуры.
Широко известно следующее высказывание Алексея Лосева, в котором удачно подчеркнута роль «золотого сечения» в греческой культуре:«С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления — Золотого Сечения... Их (древних греков – А.С.) систему космических пропорций нередко в литературе изображают как курьезный результат безудержной и дикой фантазии. В такого рода объяснениях сквозит антинаучная беспомощность тех, кто это заявляет. Однако понять данный историко-эстетический феномен можно только в связи с целостным пониманием истории, то есть, используя диалектико-материалистическое представление о культуре и ища ответа в особенностях античного общественного бытия».
Следует отметить, что строгая геометрическая формулировка знаменитой «задачи о делении отрезка в крайнем и среднем отношении» (так в древности называлась задача о «золотом сечении») впервые дана в Началах Евклида. Там же, а именно в 13-й, то есть заключительной книге своих Начал, Евклид изложил теорию Платоновых тел, которая является существенным разделом геометрической теории «золотого сечения», так как два главных Платоновых тела, додекаэдр и икосаэдр, основаны на «золотом сечении». Кстати, этот факт, то есть размещение теории правильных многогранников, лежащих в основе космологии Платона, в заключительной (то есть как бы самой главной) книге Начал Евклида, дало основание древнегреческому математику Проклу, который был комментатором Евклида, выдвинуть интересную гипотезу об истинных целях, которые преследовал Евклид, создавая свои Начала. Согласно Проклу, Евклид создавал Начала не с целью изложения геометрии как таковой, а чтобы дать полную систематизированную теорию построения «идеальных» фигур, в частности пяти Платоновых тел, попутно осветив некоторые новейшие достижения математики!
2.2. Числа Фибоначчи
В 13 в. при изучении задачи о «размножении кроликов» выдающийся итальянский математик Фибоначчи открыл рекуррентную формулу:
| F(n) = F(n-1) + F(n-2), | (1) |
которая при начальных условиях F(1) = F(2) = 1 порождает знаменитые числа Фибоначчи F(n): 1, 1, 2, 3, 5, 8, 13, 21,..., получившие в дальнейшем широкую известность, особенно в ботанике, где они выражают так называемый «закон филлотаксиса», которому подчиняются ростовые процессы многих ботанических структур [8-10].
Историческое значение формулы (1) состоит в том, что это была первая в истории математики рекуррентная формула, к которой в своих истоках восходит метод рекуррентных соотношений, ставший в дальнейшем одним из наиболее мощных методов решения комбинаторных задач. Историческое значение «задачи о кроликах» состоит в том, что эта задача дает начало «теории биологических популяций», описываемой с помощью рекуррентных соотношений.
2.3. «Божественная пропорция» Луки Пачоли
В эпоху Возрождения огромный вклад в развитие «Теории Золотого Сечения» внес знаменитый итальянский математик и ученый монах Лука Пачоли (1445-1517), друг и советник Леонардо да Винчи. Лука Пачоли пишет первое в истории науки математическое сочинение о Золотой Пропорции, названное им «De Divina Proportione» («О Божественной Пропорции») и опубликованное в 1509 г. Книга состоит из трех частей: в первой части излагаются свойства золотого сечения, вторая часть посвящена правильным многогранникам, третья – приложениям золотого сечения в архитектуре. В этой книге Пачоли, апеллируя к «Государству», «Законам», «Тимею» Платона, последовательно выводит 12 (!) различных свойств золотого сечения. Характеризуя эти свойства, Пачоли пользуется весьма сильными эпитетами: «исключительное», «превосходнейшее», «замечательное», «почти сверхъестественное» и т.п. Раскрывая данную пропорцию в качестве универсального отношения, выражающего и в природе и в искусстве совершенство красоты, он называет ее «божественной» и склонен рассматривать ее как «орудие мышления», «эстетический канон», «как принцип мира и природы». Эта книга является одним из первых математических сочинений, в котором христианская доктрина о Боге как творце Вселенной получает научное обоснование. Пачоли называет золотое сечение «божественным» и выделяет ряд свойств золотой пропорции, которые, по его мнению, присущи самому Богу.
2.4. Додекаэдро-икосаэдрическая доктрина
Среди пяти Платоновых тел особую роль играют икосаэдр и додекаэдр.
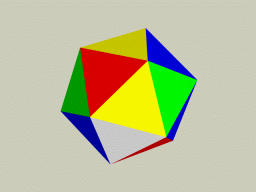
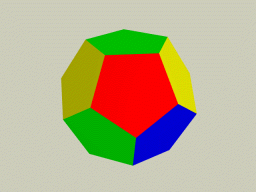
Икосаэдр и додекаэдр
Роль этих совершенных геометрических фигур, основанных на «золотом сечении», в развитии науки настолько велика, что правомерно говорить о том, что в трудах Платона возникла «икосаэдро-додекаэдрическая доктрина», которая «красной нитью» проходит через всю науку. Еще Сократ высказал предположение, что Земля имеет форму додекаэдра. Эта идея была затем развита в работах Бимона, Пуанкаре и Кислицина и привела к возникновению весьма оригинальных теорий формы Земли, имеющих важные практические приложения в геологии. В 17 в. Иоганн Кеплер, используя «Тела Платона» построил оригинальную геометрическую модель Солнечной Системы («Космический Кубок» Кеплера).
2.5. Вклад Кеплера в теорию Золотого Сечения
Гениальный астроном Иоганн Кеплер (1571-1630) был последовательным приверженцем Золотого Сечения, Платоновых тел и Пифагорейской доктрины о числовой гармонии Мироздания. Свое восхищение «золотым сечением» Кеплер выразил в словах, которые взяты эпиграфом к настоящей статье.
Считается, что именно Кеплер обратил внимание на ботаническую закономерность филлотаксиса и установил связь между числами Фибоначчи и золотой пропорцией, доказав, что последовательность отношений соседних чисел Фибоначчи:

в пределе стремится к золотой пропорции, то есть

2.6. Формула Кассини
В 17-м веке числа Фибоначчи привлекают внимание многих знаменитых ученых. Именно в этот период современник Кеплера, известный астроном Джованни Кассини (1625-1712) доказывает замечательное тождество, связывающее три соседних числа Фибоначчи:
Fn-1 Fn+1 —  = (-1)n. = (-1)n. | (2) |
Формула (2) называется формулой Кассини. Эта удивительная формула вызывает благоговейный трепет, если представить себе, что она справедлива для любого значения n = 0, ± 1, ± 2, ± 3, …, и истинное эстетическое наслаждение, потому что чередование +1 и –1 в указанном выше математическом выражении при последовательном прохождении всех чисел Фибоначчи от -Ґ до +Ґ вызывает неосознанное чувство ритма и гармонии.
2.7. Вклад Люка в теорию Золотого Сечения
Начиная с 19 в., математические работы, посвященные свойствам чисел Фибоначчи, по остроумному выражению одного математика «начали размножаться как фибоначчиевые кролики». Лидером этих исследований в 19-м веке стал французский математик Люка (1842-1891). Заслуга Люка перед теорией чисел Фибоначчи состоит в том, что он впервые ввел в широкое употребление само название числа Фибоначчи и кроме того ввел в рассмотрение так называемые обобщенные числа Фибоначчи, описываемые следующей рекуррентной формулой:
| G(n) = G(n-1) + G(n-2). | (3) |
В зависимости от начальных членов G(1), G(2) рекуррентная формула (3) порождает бесконечное количество числовых последовательностей, подобных классическим числам Фибоначчи. Из всех возможных последовательностей, порождаемых (3), наибольшее применение получили две числовые последовательности – числа Фибоначчи F(n): 1, 1, 2, 3, 5, 8, 13, 21,... и так называемые числа Люка L(n): 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199,....
2.8. Формулы Бине
В 19-м веке было сделано одно из наиболее важных математических открытий в области «Теории Золотого Сечения», а именно, открыты две математические формулы, связывающие золотую пропорцию t с числами Фибоначчи и Люка:
 | (4) |
 | (5) |
где n = 0, ± 1, ± 2, ± 3, ….
Эти формулы широко известны и называются формулами Бине в честь французского математика 19-го века Жака Филлипа Мари Бине (1786 — 1856), который первым вывел эти формулы.
Исследования Фибоначчи, Пачоли, Кеплера, Люка и Бине стали стартовой площадкой для исследований российского математика Николая Воробьева, который своей замечательной брошюрой [8], первое издание которой относится к 1961 г., привлек внимание научной общественности 20-го века к числам Фибоначчи. В 1963 г. группа американских математиков организовала Фибоначчи-ассоциация, которая поставила своей главной целью исследование математических свойств чисел Фибоначчи и их приложений в различных сферах науки и искусства.
2.9. Икосаэдр как главный геометрический объект математики
Имя немецкого математика Феликса Клейна широко известно в математических кругах. В течении многих лет он возглавил математический институт Геттингенского университета, который на протяжении первой четверти 20-го века был признанным мировым математическим центром. Основные работы Клейна посвящены неевклидовой геометрии, теории непрерывных групп, теории алгебраических уравнений, теории эллиптических функций, теории автоморфных функций. Свои идеи в области геометрии Клейн изложил в работе «Сравнительное рассмотрение новых геометрических исследований» (1872), известной под названием Эрлангенская программа.
Кроме «Эрлангенской программы» и других выдающихся математических достижений, гениальность Феликса Клейна проявилась также в том, что более 100 лет назад он сумел предсказать выдающуюся роль Платоновых тел, в частности, икосаэдра, в будущем развитии науки, в частности, математики. В 1884 г. Феликс Клейн опубликовал книгу «Лекции об икосаэдре и решении уравнений пятой степени» [11], посвященную геометрической теории икосаэдра.
Согласно Ф. Клейну, ткань математики широко и свободно разбегается листами отдельных теорий. Но есть объекты, в которых сходятся несколько листов, — своеобразные точки ветвления. Их геометрия связывает листы и позволяет охватить общематематический смысл разных теорий. Именно таким математическим объектом, по мнению Клейна, является икосаэдр. Клейн трактует икосаэдр как математический объект, из которого расходятся ветви пяти математических теорий: геометрия, теория Галуа, теория групп, теория инвариантов и дифференциальные уравнения.
Таким образом, главная идея Клейна чрезвычайно проста: каждый уникальный геометрический объект так или иначе связан со свойствами икосаэдра.
Таким образом, еще в 19-м веке гениальная интуиция Феликса Клейна привела его к мысли о том, что одна из древнейших геометрических фигур – икосаэдр – является главной геометрической фигурой математики. Тем самым Клейн в 19 в. вдохнул новую жизнь в развитие «додекаэдро-икосаэдрического представления» о структуре Вселенной, последователями которого были великие ученые и философы: Платон, построивший свою космологию на основе правильных многогранников, Евклид, посвятивший свои «Начала» изложению теории Платоновых тел, Иоганн Кеплер, использовавший Платоновы тела при создании своего Космического кубка, весьма оригинальной геометрической модели Солнечной системы.
Свежие комментарии